题目内容
14. 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )| A. | 5 | B. | $\frac{15}{2}$ | C. | $\frac{25}{4}$ | D. | $\frac{20}{3}$ |
分析 由CP⊥CQ,AB是直径,易得∠Q=∠ABC,又由tan∠ABC=$\frac{4}{3}$,易得当CP是直径,CQ最大,继而求得答案.
解答 解:∵CP⊥CQ,AB是直径,
∴∠ACB=∠PCQ=90°,
∵∠A=∠P,
∴∠Q=∠ABC,
∴tan∠Q=tan∠ABC,
∴$\frac{CP}{CQ}$=$\frac{4}{3}$,
∴当CP是直径,即CP=10时,CQ最大,最大值为:CQ=$\frac{15}{2}$.
故选B.
点评 此题考查了圆周角定理以及三角函数的定义.注意根据题意得到当CP是直径,CQ最大是关键.

练习册系列答案
相关题目
2.二元一次方程组$\left\{\begin{array}{l}{x+2y=2}\\{2x+y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$ |
6.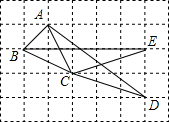 如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
 如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |
 如图,△ABD与△ACE中,AB=AC,∠ACE+∠ABD=180°,BD=CE,BC延长线交ED于F.
如图,△ABD与△ACE中,AB=AC,∠ACE+∠ABD=180°,BD=CE,BC延长线交ED于F. 如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为112.5°.
如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为112.5°.