题目内容
18. 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠CFC′=150°,则∠AED′等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠CFC′=150°,则∠AED′等于( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
分析 先根据翻折变换的性质求出∠EFC′的度数,再由平行线的性质求出∠D′EF的度数,进而可得出结论.
解答 解:∵∠CFC′=150°,
∴∠EFC′=$\frac{360°-150°}{2}$=105°.
∵ED′∥FC′,
∴∠D′EF=180°-105°=75°,
∴∠AED′=180°-2×75°=180°-150°=30°.
故选D.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
9.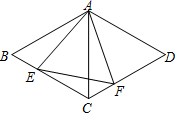 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )| A. | $4\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
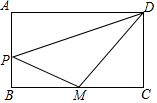 如图.长方形ABCD长为10厘米,宽为6厘米,M为BC的中点,三角形PMD面积为25平方厘米.那么三角形APD的面积为多少平方厘米?
如图.长方形ABCD长为10厘米,宽为6厘米,M为BC的中点,三角形PMD面积为25平方厘米.那么三角形APD的面积为多少平方厘米?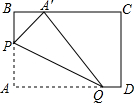 在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.
在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.