题目内容
19.阅读材料:如图(1)在任意△ABC中,点P是AB上的动点(点P异于点A、B),经过点P的直线PQ∥BC,交AC于点Q,我们不妨称这种直线为过点P的△ABC的相似线,经过进一步研究,我们发现$\frac{AP}{AB}$=$\frac{AQ}{AC}$=$\frac{PQ}{BC}$.(1)若AP=3,AB=6,BC=8,则PQ=4.
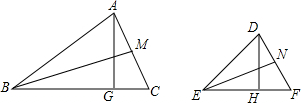
(2)如图(2),在△MGN中,∠MGN=90°,MG=3,NG=4,GH是斜边MN上的高,点E在MN上(点E不与M、N重合),过点E作EF⊥MN与△MGN的直角边相交于点F,当点E在MH上时,直线EF为过点E的△MGH是相似线,线段GH的长为$\frac{12}{5}$,线段MH的长为$\frac{9}{5}$.
(3)在(2)的条件下,设ME=x,△MEF的面积为y,当点E在斜边MN上移动时,
①求y与x的函数关系式(写出自变量x的取值范围).
②当x取何值时,y有最大值?并求出最大值.
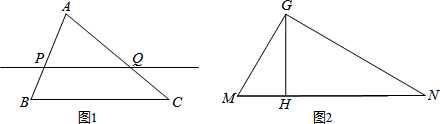
分析 (1)利用相似线的定义列出比例式,将已知长代入求出PQ的长即可;
(2)利用相似线定义判断得到EF为三角形MGH的相似线,在直角三角形GMN中,利用勾股定理求出MN的长,再利用面积法求出GH的长,在直角三角形GMH中,利用勾股定理求出MH的长即可;
(3)①分两种情况考虑:一是P在MH上;一是P在HN上,表示出y与x的函数关系式即可;
②根据x的范围,利用二次函数性质求出y的最大值,以及此时x的值即可.
解答 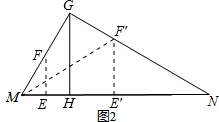 解:(1)由题意得:$\frac{AP}{AB}$=$\frac{PQ}{BC}$,即$\frac{3}{6}$=$\frac{PQ}{8}$,
解:(1)由题意得:$\frac{AP}{AB}$=$\frac{PQ}{BC}$,即$\frac{3}{6}$=$\frac{PQ}{8}$,
解得:PQ=4;
(2)当点E在MH上时,直线EF为过点E的△MGH是相似线,
在Rt△MNG中,MG=3,NG=4,
根据勾股定理得:MN=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S△MNG=$\frac{1}{2}$MG•NG=$\frac{1}{2}$MN•GH,
∴GH=$\frac{MG•NG}{MN}$=$\frac{3×4}{5}$=$\frac{12}{5}$;
线段GH的长为$\frac{12}{5}$,线段MH的长为$\frac{9}{5}$;
在Rt△MGH中,根据勾股定理得:MH=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$;
(3)①当点E在线段MH上移动,即0<x≤$\frac{9}{5}$时,
∵EF为过点E的△MGH的相似线,
∴$\frac{EF}{GH}$=$\frac{ME}{MH}$,即$\frac{EF}{\frac{12}{5}}$=$\frac{x}{\frac{9}{5}}$,
解得:EF=$\frac{4}{3}$x,
此时y=$\frac{1}{2}$ME•EF=$\frac{1}{2}$•x•$\frac{4}{3}$x=$\frac{2}{3}$x2;
当点E′在线段HN上移动,即$\frac{9}{5}$<x<5时,
∵E′F′为过点E的△GHN的相似线
∴$\frac{E′F′}{GH}$=$\frac{NE}{NH}$,即$\frac{E′F′}{\frac{12}{5}}$=$\frac{5-x}{\frac{16}{5}}$,
解得:E′F′=$\frac{3}{4}$(5-x),
此时y=$\frac{1}{2}$ME′•E′F′=$\frac{1}{2}$x•$\frac{4}{3}$(5-x)=-$\frac{2}{3}$x2+$\frac{10}{3}$x;
②当0<x≤$\frac{9}{5}$时,y=$\frac{2}{3}$x2,
当x=$\frac{9}{5}$时,y有最大值$\frac{54}{25}$;
当$\frac{9}{5}$<x<5时,y=-$\frac{2}{3}$x2+$\frac{10}{3}$x,
当x=$\frac{5}{2}$时,y有最大值$\frac{25}{6}$,
综上所述,当$\frac{5}{2}$时,y有最大值$\frac{25}{6}$.
故答案为:(1)4;(2)EF;$\frac{12}{5}$;$\frac{9}{5}$
点评 此题考查了相似形综合题,涉及的知识有:相似三角形的判定与性质,勾股定理,以及二次函数性质,熟练掌握题中的新定义:“相似线定义”是解本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 8 | B. | 10 | C. | 8或10 | D. | 12 |
 我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.
我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.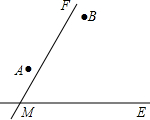 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.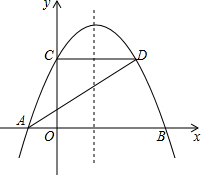 如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2). 已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.
已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.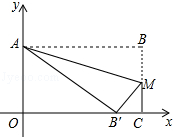 矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知
矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,OA与y轴重合,OC与x轴重合,M为BC上点,沿AM折叠矩形使得点B′落在OC上,且知