题目内容
15.已知A=-2ab,B=3ab(a+b),C=2a2b-3ab2,且a=-1,b=-$\frac{1}{2}$,求3A•B-$\frac{1}{2}$A•C.分析 先把A、B、C代入化简,然后将a=-1,b=-$\frac{1}{2}$代入计算即可.
解答 解:∵A=-2ab,B=3ab(a+b),C=2a2b-3ab2,
∴3A•B-$\frac{1}{2}$A•C=3•(-2ab)•[3ab(a+b)]-$\frac{1}{2}$•(-2ab)•(2a2b-3ab2)
=-18a3b2-18a2b3+2a3b2-3a2b3
=-16a3b2-21a2b3,
当a=-1,b=-$\frac{1}{2}$时,原式=16×$\frac{1}{4}$+21×$\frac{1}{8}$=$\frac{53}{8}$.
点评 本题考查整式的混合运算-化简求值,熟练掌握单项式乘单项式、单项式乘多项式的法则是解题的关键,属于中考常考题型.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
20. 如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
 如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
20.将分别标有数字0,1,2,3的司长卡片背面朝上洗匀后,抽取一张作为十位上的数字,再抽取一张作为个位上的数字,每次抽取都不放回,则所得的两位数恰好是奇数的概率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
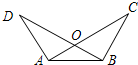 如图,已知∠D=∠C,还需添加一个条件是∠ABD=∠BAC或∠ABC=∠BAD,使得△ABD≌△BAC,依据是AAS或ASA.
如图,已知∠D=∠C,还需添加一个条件是∠ABD=∠BAC或∠ABC=∠BAD,使得△ABD≌△BAC,依据是AAS或ASA. 把线段AB先向右平移2个单位长度,再向上平移3个单位长度,得到线段CD,请画出线段CD,并写出C,D两点的坐标.
把线段AB先向右平移2个单位长度,再向上平移3个单位长度,得到线段CD,请画出线段CD,并写出C,D两点的坐标.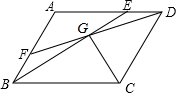 已知:在?ABCD中,E为AD上一点,F为AB上一点,且BE=DF,BE与DF交于G.
已知:在?ABCD中,E为AD上一点,F为AB上一点,且BE=DF,BE与DF交于G. 如图,两个圆的圆心相同,面积分别为8cm2、18cm2,求圆环的宽度(两圆半径之差,结果保留π).
如图,两个圆的圆心相同,面积分别为8cm2、18cm2,求圆环的宽度(两圆半径之差,结果保留π).