题目内容
15.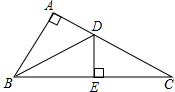 如图,已知Rt△ABC中,AB=AC、BC=10,∠A为Rt∠,BD为△ABC的一条角平分线,过点D作DE垂直于BC,求△CDE的周长.
如图,已知Rt△ABC中,AB=AC、BC=10,∠A为Rt∠,BD为△ABC的一条角平分线,过点D作DE垂直于BC,求△CDE的周长.
分析 先根据角平分线的性质得DA=DE,再证明Rt△BAD≌Rt△BED得到AB=EB,然后利用等线段代换得到△CDE的周长等于BC的长.
解答 解:∵BD为△ABC的一条角平分线,
而DA⊥AB,DE⊥BC,
∴DA=DE,
在Rt△BAD和Rt△BED中,
$\left\{\begin{array}{l}{DA=DE}\\{BD=BD}\end{array}\right.$,
∴Rt△BAD≌Rt△BED,
∴AB=EB,
∴△CDE的周长=DE+DC+CE=DA+DC+CE=AC+CE=AB+CE=BE+CE=BC=10.
点评 本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了等腰三角形的性质.

练习册系列答案
相关题目
10.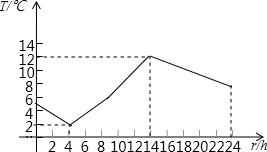 如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )
如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )
 如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )
如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )| A. | 10℃ | B. | -10℃ | C. | 8℃ | D. | 12℃ |
 如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的距离s(km)和行驶时间t(h)之间的关系,请根据图象回答下列问题:
如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的距离s(km)和行驶时间t(h)之间的关系,请根据图象回答下列问题: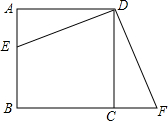 如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF
如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF