��Ŀ����
6����Rt��ABC�У���BAC=90�㣬BC=10��tan��ABC=$\frac{3}{4}$����O��AB���϶��㣬��OΪԲ�ģ�OBΪ�뾶�ġ�O���BC����һ����ΪD������D��AB�Ĵ��ߣ�����O�ڵ�E������BE��AE��1����AE��BC����ͼ��1����ʱ�����O�İ뾶����
��2����BO=x��AE=y����y����x�ĺ�����ϵʽ����д��������
��3������AΪԲ�ĵġ�A���O�й�����D��E������Aǡ��Ҳ����Cʱ����DE�ij���
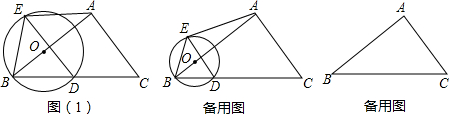
���� ��1������O��OG��BD��G����AB��DE�Ľ���ΪF����ͼ��1������֤��AEF�ա�BDF���ı���AEDC��ƽ���ı��Σ��Ӷ��ɵ�BD=DC=5�����ݴ��������ɵ�BG=DG=$\frac{1}{2}$BD=$\frac{5}{2}$��Ȼ����Rt��BGO���������Ǻ������ɶ������������O�İ뾶����
��2������A��AH��BC��H����ͼ��2�����������Ǻ��������ɶ���������������AC��AB��AH��BH��CH�����ݴ��������ɵ�DF=EF���ٸ����߶δ�ֱƽ���ߵ����ʿɵ�AE=AD��Ȼ����Rt��BGO���������Ǻ������ɶ��������BG����x�Ĵ���ʽ��ʾ������������x�Ĵ���ʽ���α�ʾ��BD��DH��AD��AE��������Խ����
��3��������D��H����ߣ���ͼ��2�������ݵ��������ε����ʿɵ�DH=CH���Ӷ��������BD��DF��DE�ij���������D��H���ұߣ����D���C�غϣ��Ӷ����������BD��DF��DE�ij���
��� �⣺��1������O��OG��BD��G�� ��AB��DE�Ľ���ΪF����ͼ��1����
��AB��DE�Ľ���ΪF����ͼ��1����
��OG��BD��G��
��BG=DG��
��DE��AB��
��EF=DF��
��AE��BC��
���AEF=��BDF��
�ڡ�AEF�͡�BDF�У�
$\left\{\begin{array}{l}{��AEF=��BDF}\\{EF=DF}\\{��AFE=��BFD}\end{array}\right.$��
���AEF�ա�BDF��
��AE=BD��
�ߡ�BFD=��BAC=90�㣬
��DE��AC��
��AE��BC��
���ı���AEDC��ƽ���ı��Σ�
��AE=DC��
��BD=DC=$\frac{1}{2}$BC=5��
��BG=DG=$\frac{1}{2}$BD=$\frac{5}{2}$��
��Rt��BGO��
tan��OBG=$\frac{OG}{BG}$=$\frac{3}{4}$��
��OG=$\frac{3}{4}$BG=$\frac{3}{4}$��$\frac{5}{2}$=$\frac{15}{8}$��
��OB=$\sqrt{B{G}^{2}+O{G}^{2}}$=$\sqrt{��\frac{5}{2}��^{2}+��\frac{15}{8}��^{2}}$=$\frac{25}{8}$��
���O�İ뾶��Ϊ$\frac{25}{8}$��
��2������A��AH��BC��H����ͼ��2����
��Rt��BAC��
tan��ABC=$\frac{AC}{AB}$=$\frac{3}{4}$��
��AC=3k����AB=4k��
��BC=5k=10��
��k=2��
��AC=6��AB=8��
��AH=$\frac{AB•AC}{BC}$=$\frac{8��6}{10}$=$\frac{24}{5}$��
��BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{��8+\frac{24}{5}����8-\frac{24}{5}��}$=$\frac{32}{5}$��
��HC=BC-BH=10-$\frac{32}{5}$=$\frac{18}{5}$��
��AB��DE��
����ݴ��������ɵ�DF=EF��
��AB��ֱƽ��DE��
��AE=AD��
��Rt��BGO��
tan��OBG=$\frac{OG}{BG}$=$\frac{3}{4}$��
��OG=$\frac{3}{4}$BG��
��OB=$\sqrt{O{G}^{2}+B{G}^{2}}$=$\sqrt{��\frac{3}{4}BG��^{2}+B{G}^{2}}$=$\frac{5}{4}$BG=x��
��BG=$\frac{4}{5}$x��
��BD=2BG=$\frac{8}{5}x$��
��DH=BH-BD=$\frac{32}{5}$-$\frac{8}{5}$x��
��y=AE=AD=$\sqrt{D{H}^{2}+A{H}^{2}}$
=$\sqrt{��\frac{32}{5}-\frac{8}{5}x��^{2}+��\frac{24}{5}��^{2}}$
=$\sqrt{\frac{64}{25}{x}^{2}-\frac{512}{25}x+64}$
=$\frac{8\sqrt{{x}^{2}-8x+5}}{5}$��0��x��$\frac{25}{4}$����
��3��������D��H����ߣ���ͼ��2����
��AD=AC��AH��DC��
��DH=CH=$\frac{18}{5}$��
��BD=BH-DH=$\frac{32}{5}$-$\frac{18}{5}$=$\frac{14}{5}$��
��Rt��BFD��
tan��FBD=$\frac{DF}{BF}$=$\frac{3}{4}$��
��BF=$\frac{4}{3}$DF��
��BD=$\sqrt{B{F}^{2}+D{F}^{2}}$
=$\sqrt{��\frac{4}{3}DF��^{2}+D{F}^{2}}$
=$\frac{5}{3}$DF=$\frac{14}{5}$��
��DF=$\frac{42}{25}$��
��DE=2DF=$\frac{84}{25}$��
������D��H���ұߣ�
���D���C�غϣ�
��BD=BC=10��
��$\frac{5}{3}$DF=10��
��DF=6��
��DE=2DF=12��
��������������Aǡ��Ҳ����Cʱ��DE�ij�Ϊ$\frac{84}{25}$��12��
���� ������Ҫ�����˴���������ȫ�������ε��ж������ʡ�ƽ���ı��ε��ж������ʡ����Ǻ��������ɶ��������������ε����ʡ��߶δ�ֱƽ���ߵ����ʵ�֪ʶ���ڽ������Ĺ������õ��˷������ۡ����������Ҫ����ѧ˼�뷽������һ�����Ѷȣ���AEת��ΪAD�ǽ���ڣ�2��С��Ĺؼ������÷������۵�˼���ǽ���ڣ�3��С��Ĺؼ���

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{3}}{2}$ |
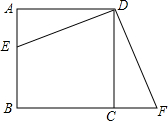 ��ͼ����������ABCD�У���E��AB���ϣ���F��BC�ߵ��ӳ����ϣ���AE=CF
��ͼ����������ABCD�У���E��AB���ϣ���F��BC�ߵ��ӳ����ϣ���AE=CF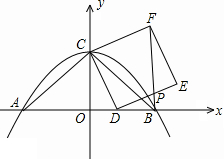 ��ͼ��������y=-$\frac{1}{4}$x2+4��x���ڵ�A��B����y���ڵ�C������AC��BC��D���߶�OB��һ���㣬��CDΪһ�����Ҳ���������CDEF������BF����DE�ڵ�P��
��ͼ��������y=-$\frac{1}{4}$x2+4��x���ڵ�A��B����y���ڵ�C������AC��BC��D���߶�OB��һ���㣬��CDΪһ�����Ҳ���������CDEF������BF����DE�ڵ�P��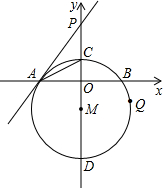 ��ͼ����ֱ������ϵ�У���M��Բ��M��y���ϣ���M��x�ύ�ڵ�A��B����y�ύ�ڵ�C��D������A����M������AP��y���ڵ�P������M�İ뾶Ϊ5����A������Ϊ��-4��0����
��ͼ����ֱ������ϵ�У���M��Բ��M��y���ϣ���M��x�ύ�ڵ�A��B����y�ύ�ڵ�C��D������A����M������AP��y���ڵ�P������M�İ뾶Ϊ5����A������Ϊ��-4��0����