题目内容
17.(1)计算:$\sqrt{9a}$+$\sqrt{4b}$-$\sqrt{\frac{a}{4}}$+$\sqrt{b}$;(2)若a=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,b=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$,求(1)中代数式的值.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先利用分母有理化得到a=($\sqrt{2}$-1)2,b=($\sqrt{2}$+1)2,再把a、b的值代入$\frac{5\sqrt{a}}{2}$+3$\sqrt{b}$中,然后根据二次根式的性质化简后合并即可.
解答 解:(1)原式=3$\sqrt{a}$+2$\sqrt{b}$-$\frac{\sqrt{a}}{2}$+$\sqrt{b}$
=$\frac{5\sqrt{a}}{2}$+3$\sqrt{b}$;
(2)a=($\sqrt{2}$-1)2,b=($\sqrt{2}$+1)2,
原式=$\frac{5}{2}$×($\sqrt{2}$-1)+3($\sqrt{2}$+1)
=$\frac{11\sqrt{2}+1}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.

练习册系列答案
相关题目
12.某校九年级学生中有女生226人,男生250人,计划组成甲、乙两种活动小组共40个,甲、乙两种活动小组每组的人数搭配情况如表:
设准备组成x个甲种活动小组,请解答下列问题:
(1)求x的值,并说明有哪几种符合题意的建立活动小组的方案;
(2)若甲种活动每组需要培训费50元,乙种活动每组需要培训费40元,说明(1)中哪种方案能节省经费,并计算最少经费为多少元.
| 需要女生 | 需要男生 | |
| 甲种活动 | 7人 | 4人 |
| 乙种活动 | 3人 | 10人 |
(1)求x的值,并说明有哪几种符合题意的建立活动小组的方案;
(2)若甲种活动每组需要培训费50元,乙种活动每组需要培训费40元,说明(1)中哪种方案能节省经费,并计算最少经费为多少元.
18.tan30°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
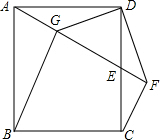 如图,已知在正方形ABCD中,点E在CD边长,过C点作AE的垂线交于点F,联结DF,过点D作DF的垂线交A于点G,联结BG.
如图,已知在正方形ABCD中,点E在CD边长,过C点作AE的垂线交于点F,联结DF,过点D作DF的垂线交A于点G,联结BG.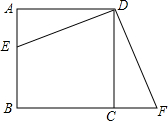 如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF
如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF