题目内容
4. 如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )| A. | (8,4) | B. | (8,2) | C. | (4,2) | D. | (4,8) |
分析 由△OCD与△OAB的面积之比为1:4,△OCD∽△OAB,推出CD:AB=OD:OB=1:2,由C(2,1),D(2,0),推出OD=2,CD=1,
推出OB=4,AB=2,即可解决问题.
解答 解:∵△OCD与△OAB的面积之比为1:4,△OCD∽△OAB,
∴CD:AB=OD:OB=1:2,
∵C(2,1),D(2,0),
∴OD=2,CD=1,
∴OB=4,AB=2,
∴A(4,2).
点评 此题考查了位似变换,位似变换的两个图形相似,相似三角形的性质,解题的关键是记住相似三角形的面积比等于相似比的平方,属于中考常考题型.

练习册系列答案
相关题目
9.代数式-4xy2+xy+1是( )
| A. | 二次二项式 | B. | 二次三项式 | C. | 三次二项式 | D. | 三次三项式 |
13.无论k为何实数,二次函数y=x2-(3-k)x+k的图象总是过定点( )
| A. | (-1,4) | B. | (1,0) | C. | (1,4) | D. | (-1,0) |
14.某商品在元旦假日准备开展促销活动,商品的标价为1000元,4折销售后任可赚80元,则该商品的成本价为( )
| A. | 400元 | B. | 440元 | C. | 320元 | D. | 270元 |
 如图,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,求出这两个角的度数?设∠ABD和∠DBC的度数分别为x°,y°,根据题意所列方程组是$\left\{\begin{array}{l}{x+y=90}\\{x=2y-15}\end{array}\right.$.
如图,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,求出这两个角的度数?设∠ABD和∠DBC的度数分别为x°,y°,根据题意所列方程组是$\left\{\begin{array}{l}{x+y=90}\\{x=2y-15}\end{array}\right.$. 如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,∠D=60°,则∠C的度数为40°.
如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,∠D=60°,则∠C的度数为40°.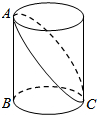 如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.
如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.