题目内容
15.先化简,再求代数式$\frac{{x}^{2}-2x+1}{{x}^{3}-x}$÷(1-$\frac{1}{x}$)的值,其中x=2sin45°-tan45°.分析 先化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:$\frac{{x}^{2}-2x+1}{{x}^{3}-x}$÷(1-$\frac{1}{x}$)
=$\frac{(x-1)^{2}}{x(x+1)(x-1)}÷\frac{x-1}{x}$
=$\frac{x-1}{x(x+1)}×\frac{x}{x-1}$
=$\frac{1}{x+1}$,
当x=2sin45°-tan45°=2×$\frac{\sqrt{2}}{2}$-1=$\sqrt{2}-1$,
原式=$\frac{1}{\sqrt{2}-1+1}=\frac{\sqrt{2}}{2}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
20. 如图所示的扇形图是对某班学生知道父母生日情况的调查,A表示只知道父亲生日,B表示只知道母亲生日,C表示知道父母两人的生日,D表示都不知道,若该班有40名学生,则只知道母亲生日的人数有( )人.
如图所示的扇形图是对某班学生知道父母生日情况的调查,A表示只知道父亲生日,B表示只知道母亲生日,C表示知道父母两人的生日,D表示都不知道,若该班有40名学生,则只知道母亲生日的人数有( )人.
 如图所示的扇形图是对某班学生知道父母生日情况的调查,A表示只知道父亲生日,B表示只知道母亲生日,C表示知道父母两人的生日,D表示都不知道,若该班有40名学生,则只知道母亲生日的人数有( )人.
如图所示的扇形图是对某班学生知道父母生日情况的调查,A表示只知道父亲生日,B表示只知道母亲生日,C表示知道父母两人的生日,D表示都不知道,若该班有40名学生,则只知道母亲生日的人数有( )人.| A. | 25% | B. | 10 | C. | 22 | D. | 25 |
7.已知方程x2+mx+3=0的一个根是1,则m的值为( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
4. 如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
 如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )| A. | (8,4) | B. | (8,2) | C. | (4,2) | D. | (4,8) |
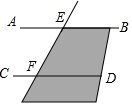 如图,直线AB、CD被直线EF所截,AB∥CD,点P是阴影部分上一个动点(点P不在直线AB、CD、EF上),那么∠EPF,∠PEB,∠PFD三者之间的等量关系是∠EPF=∠BEP+∠PFD或∠EPF=∠BEP-∠PFD.
如图,直线AB、CD被直线EF所截,AB∥CD,点P是阴影部分上一个动点(点P不在直线AB、CD、EF上),那么∠EPF,∠PEB,∠PFD三者之间的等量关系是∠EPF=∠BEP+∠PFD或∠EPF=∠BEP-∠PFD.