题目内容
16.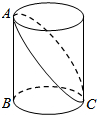 如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.
如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.
分析 要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
解答  解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为4dm,圆柱高为3dm,
∴AB=3dm,BC=BC′=3dm,
∴AC2=32+22=13,
∴AC=$\sqrt{13}$dm.
∴这圈金属丝的周长最小为2AC=2$\sqrt{13}$dm.
故答案为:2$\sqrt{13}$.
点评 本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题把圆柱的侧面展开成矩形,“化曲面为平面”是解题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
7.已知方程x2+mx+3=0的一个根是1,则m的值为( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
4. 如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
 如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )
如图,在平面直角坐标系中,以点为位似中心,将△OCD放大得到△OAB,点C、D的坐标分别为(2,1)、(2,0),且△OCD与△OAB的面积之比为1:4,则点A的坐标为( )| A. | (8,4) | B. | (8,2) | C. | (4,2) | D. | (4,8) |
1.边长为a的正三角形的内切圆的半径为( )
| A. | $\frac{1}{2}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\frac{\sqrt{3}}{3}$a | D. | $\frac{\sqrt{3}}{6}$a |
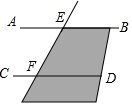 如图,直线AB、CD被直线EF所截,AB∥CD,点P是阴影部分上一个动点(点P不在直线AB、CD、EF上),那么∠EPF,∠PEB,∠PFD三者之间的等量关系是∠EPF=∠BEP+∠PFD或∠EPF=∠BEP-∠PFD.
如图,直线AB、CD被直线EF所截,AB∥CD,点P是阴影部分上一个动点(点P不在直线AB、CD、EF上),那么∠EPF,∠PEB,∠PFD三者之间的等量关系是∠EPF=∠BEP+∠PFD或∠EPF=∠BEP-∠PFD.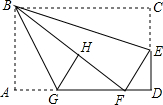 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: