题目内容
9.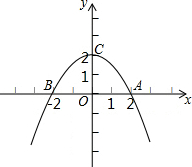 已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:
已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:(1)m的值与抛物线的函数表达式.
(2)在抛物线上是否存在另一点M,使△MAC≌△OAC?若存在求出点M的坐标;若不存在,说明理由.
分析 (1)令x=0求出y的值得到OC的长度,然后表示出OA得到点A的坐标,再把A点坐标代入解析式得到关于m的方程,则解方程求出m的值,即可得到抛物线解析式;
(2)利用△OAC是以AC为斜边的等腰直角三角形,根据全等三角形的判定,当△MAC是以AC为斜边的等腰直角三角形时,△MAC≌△OAC,则点M为AC的垂直平分线与抛物线的交点,易得此时点M不能使△MAC为直角三角形,所以可判断在抛物线上不存在另一点M,使△MAC≌△OAC.
解答 解:(1)∵x=0,y=-$\frac{1}{2}$x2+m-3=m-3,
∴C(0,m-3),
∵OA=OC=m-3,
∴A(m-3,0),
把A(m-3,0)代入y=-$\frac{1}{2}$x2+m-3得-$\frac{1}{2}$(m-3)2+m-3=0,解得m1=5,m2=3(舍去),
∴m的值为5,
∴抛物线为y=-$\frac{1}{2}$x2+2;
(2)在抛物线上不存在另一点M,使△MAC≌△OAC.理由如下:
∵△OAC是以AC为斜边的等腰直角三角形,
∴当△MAC是以AC为斜边的等腰直角三角形时,△MAC≌△OAC,
则点M为AC的垂直平分线与抛物线的交点,于是此时△MAC不能为直角三角形,
∴在抛物线上不存在另一点M,使△MAC≌△OAC.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了全等三角形的判定.

练习册系列答案
相关题目
17.已知圆的半径为r,圆心到直线a的距离为d,d和r分别是方程x2-7x+10=0的两根,则直线a与圆的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相交或相离 | D. | 相离 |
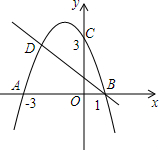 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.
如图,AB,CD相交于点O,点E,F在AB上,AE=BF,AD=BC,AD∥BC.求证:OE=OF.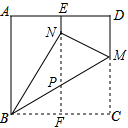 在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.
在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.