题目内容
14.如图1,某灌溉设备的喷头B高出地面1.25m,喷出的抛物线形水流在与喷头底部A的距离为1m处达到距地面最大高度2.25m,以地面所在直线为横轴,抛物线的对称轴为纵轴,建立如图2所示的平面直角坐标系.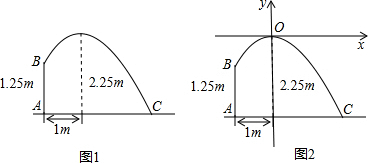
(1)求出与该抛物线水流对应的二次函数关系式;
(2)求喷出的水流离A最远的距离,即求AC的长.
分析 (1)根据题意设抛物线水流对应的二次函数关系式为y=ax2,表示出B点的坐标,代入即可;
(2)由题意得到C点的纵坐标,代入解析式求出C点的横坐标,即可求解.
解答 解:(1)设抛物线水流对应的二次函数关系式为y=ax2,
根据题意可得B点与x轴的距离为1m,故B点的坐标为(-1,-1),
代入y=ax2得-1=a•(-1)2,
∴a=-1,
所以抛物线水流对应的二次函数关系式为y=-x2;
(2)根据题意可得C点与y轴的距离为2.25m,故C点的纵坐标为-2.25,
代入y=-x2得-2,25=-x2,
解得:x=±1.5,
∴C点的纵坐标为(1.5,-2.25),
∴AC=1.5+1=2.5.
点评 本题主要考查了用待定系数法求二次函数解析式,由函数解析式求坐标,解题的关键是根据实际问题正确设出解析式和表示出点的坐标.

练习册系列答案
相关题目
 如图,在△ABC中,BC=AC,将△ABC沿CD折叠(D在AB上),使得点A与点B恰好重合,如果AB=8cm,则BD=4cm.
如图,在△ABC中,BC=AC,将△ABC沿CD折叠(D在AB上),使得点A与点B恰好重合,如果AB=8cm,则BD=4cm.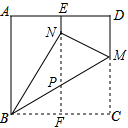 在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.
在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.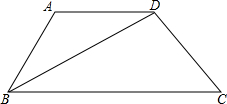 如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.
如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.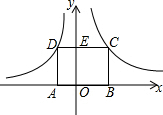 如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.
如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.