题目内容
17.如图,在?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=4,将△ABC沿直线AC翻折180°后与原图形在同一平面内,若点B的落点记为B′,则DB′的长为( )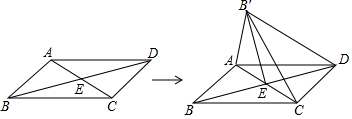
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{5}$ |
分析 如图,连接BB′.根据折叠的性质知△BB′E是等腰直角三角形,则BB′=$\sqrt{2}$BE.又B′E是BD的中垂线,则DB′=BB′.
解答 解: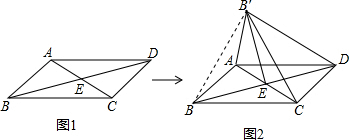 ∵四边形ABCD是平行四边形,BD=4,
∵四边形ABCD是平行四边形,BD=4,
∴BE=$\frac{1}{2}$BD=2.
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,则BB′=$\sqrt{2}$BE=2$\sqrt{2}$.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=2$\sqrt{2}$.
故选A.
点评 此题考查了平行四边形的性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
9. 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(2)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
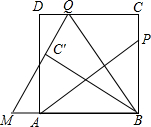 如图,P为正方形ABCD的边BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′,交BA的延长线于点M,当AB=3,BP=2PC时,QM=$\frac{13}{4}$.
如图,P为正方形ABCD的边BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′,交BA的延长线于点M,当AB=3,BP=2PC时,QM=$\frac{13}{4}$.

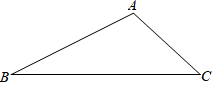 如图,已知△ABC,请用尺规作图,在BC上找一点M,使得AM+MC=BC(保留作图痕迹,不写作法).
如图,已知△ABC,请用尺规作图,在BC上找一点M,使得AM+MC=BC(保留作图痕迹,不写作法).