题目内容
15.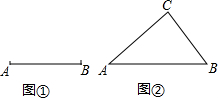 定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“奇异三角形”,这条中线为“奇异中线”.
定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“奇异三角形”,这条中线为“奇异中线”.(1)请根据定义解答:
①判断,命题:“如果直角三角形是奇异三角形,那么奇异中线一定是较长直角边上的中线”是真命题还是假命题;
②请用直尺和圆规在图①中画一个以AB为边的“奇异三角形”;
(2)如图②,在Rt△ABC中,∠C=90°,$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,求证:△ABC是“奇异三角形”.
(3)已知,等腰△ABC是“奇异三角形”,AB=AC=20,求底边BC的长.(结果保留根号)
分析 (2)①根据“奇异中线”的定义以及直角三角形的性质进行判断,即可得出结论;②作线段AB的中垂线,交AB于D,以D为圆心AB长为半径画弧,在弧上取一点C,连接AC,BC,则△ABC即为所求;
(2)取AC的中点D,连结BD,设AC=2x,则CD=AD=x,BC=$\sqrt{3}$x,在Rt△BCD中,根据勾股定理求得BD=2x,即可得出BD=AC,即△ABC是“奇异三角形”;
(3)需要分两种情况:①当腰上的中线BD=AC时,则AB=BD,过B作BE⊥AD于E,根据等腰三角形的性质以及勾股定理,即可求得BC的长;②当底边上的中线AD=BC时,则AD⊥BC,且AD=2BD,根据等腰三角形的性质以及勾股定理,列出方程,即可求得BC的长.
解答 解:(1)①∵直角三角形斜边上的中线等于斜边的一半,直角三角形较短直角边上的中线大于较长直角边,
∴如果直角三角形是奇异三角形,那么奇异中线一定是较长直角边上的中线,
∴该命题是真命题;
②如图①,作线段AB的中垂线,交AB于D,以D为圆心AB长为半径画弧,在弧上取一点C,连接AC,BC,则△ABC即为所求;
(2)证明:如图②,取AC的中点D,连结BD,
设AC=2x,则CD=AD=x,
∵$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,
∴BC=$\sqrt{3}$x,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{(\sqrt{3}x)^{2}+{x}^{2}}$=2x,
∴BD=AC,
∴△ABC是“奇异三角形”;
(3)分两种情况:
如图③,当腰上的中线BD=AC时,则AB=BD,过B作BE⊥AD于E,
∵AB=AC=20,
∴BD=20,ED=$\frac{1}{2}$AD=$\frac{1}{4}$AC=5,
∴CE=10+5=15,
∴Rt△BDE中,BE2=BD2-DE2=375,
∴Rt△BCE中,BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{375+225}$=$\sqrt{600}$=10$\sqrt{6}$;
如图④,当底边上的中线AD=BC时,则AD⊥BC,且AD=2BD,
设BD=x,则x2+(2x)2=202,
∴x2=80,
又∵x>0,
∴x=$\sqrt{80}$=4$\sqrt{5}$,
∴BC=2x=8$\sqrt{5}$.
综上所述,底边BC的长为10$\sqrt{6}$或8$\sqrt{5}$.
点评 本题属于三角形综合题,主要考查了等腰三角形的性质,勾股定理,二次根式的化简以及中线定义的综合应用,解决问题的关键是运用等腰三角形三线合一的性质以及勾股定理进行计算求解.解题时注意:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

 如图,拟从点A修建一条小径到边BC,若要使修建小径使用的材料最少,则过点A作AD⊥BC于点D,线段AD即为所求小径的位置,这样画的理由是垂线段最短.
如图,拟从点A修建一条小径到边BC,若要使修建小径使用的材料最少,则过点A作AD⊥BC于点D,线段AD即为所求小径的位置,这样画的理由是垂线段最短.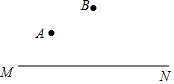 A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.
A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.