题目内容
17.(1)计算:|-2|-(-$\sqrt{2}$)0+($\frac{1}{3}$)-1.(2)解不等式组:$\left\{\begin{array}{l}{x-2<0}\\{5x+1>2(x-1)}\end{array}\right.$,并在数轴上表示出其解集.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,最后一项利用负指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即为不等式组的解集,表示在数轴上即可.
解答 解:(1)原式=2-1+3=4;
(2)$\left\{\begin{array}{l}{x-2<0①}\\{5x+1>2(x-1)②}\end{array}\right.$,
由①得:x<2,
由②得:x>-1,
∴不等式组的解集为-1<x<2,
表示在数轴上,如图所示,
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列计算正确的是( )
| A. | a8÷a4=a2 | B. | x2+x3=x5 | C. | (-c3)•(-c)5=c8 | D. | (-x-y)(-x+y)=-x2+y2 |
8.下列根式是最简二次根式的是( )
| A. | $\sqrt{0.2m}$ | B. | $\sqrt{12a-12b}$ | C. | $\sqrt{15}$ | D. | $\sqrt{\frac{a}{2}}$ |
5.已知,在河的两岸有A,B两个村庄,河宽为4千米,A、B两村庄的直线距离AB=10千米,A、B两村庄到河岸的距离分别为1千米、3千米,计划在河上修建一座桥MN垂直于两岸,M点为靠近A村庄的河岸上一点,则AM+BN的最小值为( )
| A. | 2$\sqrt{13}$ | B. | 1+3$\sqrt{5}$ | C. | 3+$\sqrt{37}$ | D. | $\sqrt{85}$ |
2.下列命题中,正确的有( )
①平分弦的直径垂直于弦;
②三角形的三个顶点确定一个圆;
③圆内接四边形的对角相等;
④圆的切线垂直于过切点的半径;
⑤过圆外一点所画的圆的两条切线长相等.
①平分弦的直径垂直于弦;
②三角形的三个顶点确定一个圆;
③圆内接四边形的对角相等;
④圆的切线垂直于过切点的半径;
⑤过圆外一点所画的圆的两条切线长相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.-3的绝对值等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | ±3 | D. | 3 |
6.根据如图所示程序计算函数值,若输入的x的值为$\frac{5}{2}$,则输出的函数值为( )
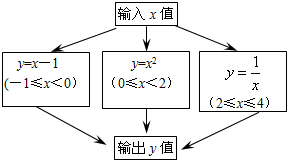

| A. | $\frac{2}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{25}$ | D. | $\frac{25}{4}$ |
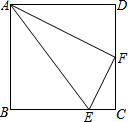 如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,
如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,