题目内容
20.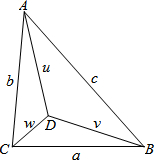 已知,如图,△ABC的三条边BC=a,CA=b,AB=c,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=u,DB=v,DC=w.
已知,如图,△ABC的三条边BC=a,CA=b,AB=c,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=u,DB=v,DC=w.(1)若∠CBD=18°,则∠BCD=42°;
(2)将△ACD绕点A顺时针方向旋转90°到△AC'D',画出△AC'D',若∠CAD=20°,求∠CAD'度数;
(3)试画出符合下列条件的正三角形:M为正三角形内的一点,M到正三角形三个顶点的距离分别为a、b、c,且正三角形的边长为u+v+w,并给予证明.
分析 (1)利用三角形的内角和即可得出结论;
(2)根据旋转的性质即可画出图形,利用旋转角即可得出结论;
(3)先构造等边三角形BDE,BCF,再判断出A、D、E、F四点均在一条直线上,另为判断出△AFC≌△GFB(SAS),即可得出结论.
解答 解:(1)在△BCD中,∠BDC=120°,∠CBD=18°,
根据三角形的内角和得,∠BCD=180°-∠BDC-∠CBD=42°,
故答案为42,
(2)画图如图1所示, 由旋转知∠DAD'=90°,
由旋转知∠DAD'=90°,
∵∠CAD=20°,
∴∠CAD'=∠DAD'-∠CAD=90°-20°=70°;
(3)画图如图2,
将△BDC绕点B按逆时针方向旋转60°,
到△BEF的位置.
连结DE,CF,
由旋转可知,△BDE和△BCF均为等边三角形,
∴DE=v,CF=a.
∵∠ADB=120°,∠BDE=60°,
即∠ADE=180°,
则A、D、E三点共线(即该三点在同一条直线上).
同理,∵∠BEF=∠BDC=120°,∠BED=60°,
即∠DEF=180°,则D、E、F三点共线,
∴A、D、E、F四点均在一条直线上.
∵EF=DC=w,
∴线段AF=u+v+w.
以线段AF为边在点B一侧作等边△AFG,
则△AFG即为符合条件的等边三角形,其中的点B即为点M.
正三角形的边长为u+v+w已证,BA=c,BF=BC=a,
下面再证BG=b.
∵∠CFB=∠AFG=60°,
即∠1+∠EFB=∠2+∠EFB=60°,
∴∠1=∠2.
在△AFC和△GFB中,
∵FA=FG,∠1=∠2,FC=FB,
∴△AFC≌△GFB(SAS),
∴AC=GB,即BG=CA=b.
从而点B(M)到等边△AFG三个顶点的距离分别为a、b、c,
且其边长为u+v+w.
点评 此题是几何变换综合题,主要考查了三角形的内角和,旋转的性质,等边三角形的性质和判定,全等三角形的判定和性质,解本题的关键是构造出等边三角形.

 全优点练单元计划系列答案
全优点练单元计划系列答案 如图,已知:∠3=∠4,那么下列结论中,正确的是( )
如图,已知:∠3=∠4,那么下列结论中,正确的是( )| A. | ∠C=∠D | B. | AD∥BC | C. | ∠1=∠2 | D. | AB∥CD |
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
| A. | 你最喜欢的篮球队将夺得CBA冠军 | |
| B. | 打开电视,正在播《最强大脑》 | |
| C. | 任意买一张电影票,座位号是2的倍数 | |
| D. | 太阳从东方升起 |
| A. | 13 | B. | 17 | C. | 13或17 | D. | 以上都不是 |
| A. | 向左平移2个单位 | B. | 向右平移2个单位 | C. | 向上平移2个单位 | D. | 向下平移2个单位 |
 如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.