题目内容
9.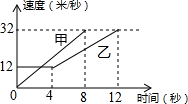 如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )| A. | 乙前4秒行驶的路程为48米 | |
| B. | 在0到8秒内甲的速度每秒增加4米 | |
| C. | 在4至8秒内甲的速度都大于乙的速度 | |
| D. | 两车到第3秒时行驶的路程相等 |
分析 前4s内,乙的速度-时间图象是一条平行于x轴的直线,即速度不变,速度×时间=路程.
甲是一条过原点的直线,则速度均匀增加;
求出两图象的交点坐标,3秒时两速度大小相等,3s前甲的图象在乙的下方,所以3秒前路程不相等;
图象在上方的,说明速度大.
解答 解:A、根据图象可得,乙前4秒的速度不变,为12米/秒,则行驶的路程为12×4=48米,故A正确;
B、根据图象得:在0到8秒内甲的速度是一条过原点的直线,即甲的速度从0均匀增加到32米/秒,则每秒增加$\frac{32}{8}$=4米秒/,故B正确;
C、在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,故C正确;
D、由于甲的图象是过原点的直线,斜率为4,所以可得v=4t(v、t分别表示速度、时间),将v=12m/s代入v=4t得t=3s,则t=3s前,甲的速度小于乙的速度,所以两车到第3秒时行驶的路程不相等,故D错误;
故选D.
点评 此题考查了函数的图形,通过此类题目的练习,可以培养学生分析问题和运用所学知识解决实际问题的能力,能使学生体会到函数知识的实用性.

练习册系列答案
相关题目
14.把分式$\frac{2x+3y}{{x}^{2}-{y}^{2}}$的x、y均扩大为原来的10倍后,则分式的值( )
| A. | 为原分式值的$\frac{1}{10}$ | B. | 为原分式值的$\frac{1}{100}$ | ||
| C. | 为原分式值的10倍 | D. | 不变 |
18.若关于x的一元二次方程x2-x+a=0有实根,则a的值可以是( )
| A. | 2 | B. | 1 | C. | 0.5 | D. | 0 |
 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m,鸡场的面积能达到180m2吗?如果能,请你给出设计方案;如果不能,请说明理由.
如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m,鸡场的面积能达到180m2吗?如果能,请你给出设计方案;如果不能,请说明理由. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=$\frac{k}{x}$的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,求此反比例函数的解析式.
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=$\frac{k}{x}$的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,求此反比例函数的解析式.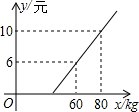 某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):
某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示): 已知:一次函数图象如图:
已知:一次函数图象如图: