题目内容
14.把分式$\frac{2x+3y}{{x}^{2}-{y}^{2}}$的x、y均扩大为原来的10倍后,则分式的值( )| A. | 为原分式值的$\frac{1}{10}$ | B. | 为原分式值的$\frac{1}{100}$ | ||
| C. | 为原分式值的10倍 | D. | 不变 |
分析 根据分式的基本性质即可求出答案.
解答 解:x、y均扩大为原来的10倍后,
∴$\frac{10(2x+3y)}{100({x}^{2}-{y}^{2})}$=$\frac{1}{10}×\frac{2x+3y}{{x}^{2}-{y}^{2}}$
故选(A)
点评 本题考查分式的基本性质,解题的关键是熟练运用分式的基本性质,本题属于基础题型.

练习册系列答案
相关题目
9.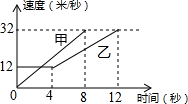 如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
 如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )| A. | 乙前4秒行驶的路程为48米 | |
| B. | 在0到8秒内甲的速度每秒增加4米 | |
| C. | 在4至8秒内甲的速度都大于乙的速度 | |
| D. | 两车到第3秒时行驶的路程相等 |
19.四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AB∥CD;②AB=CD;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
4.下列不等式中一定成立的是( )
| A. | 5a>4a | B. | -a>-2a | C. | a+2<a+3 | D. | $\frac{2}{a}$<$\frac{3}{a}$ |
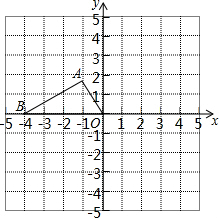 如图,A、B两点的坐标分别是A (-1,$\sqrt{3}$),B (-3,0)
如图,A、B两点的坐标分别是A (-1,$\sqrt{3}$),B (-3,0)