题目内容
19.已知菱形ABCD的周长是200,其中一条对角线长60.(1)求另一条对角线的长度.
(2)求菱形ABCD的面积.
分析 (1)由周长可求得AB的长,不妨设AC=60,AC、BD交于点O,在Rt△AOB中可求得OB,则可求得BD的长;
(2)由菱形的面积公式可求得答案.
解答  解:
解:
(1)如图,设AC、BD交于点O,不妨设AC=60,
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,AO=OC,BO=OD,且AC⊥BD,
∵菱形的周长为200,AC=60,
∴AB=50,AO=30,
在Rt△AOB中,由勾股定理可求得OB=40,
∴BD=2OB=80,即菱形的另一条对角线的长为40;
(2)由(1)可知AC=60,BD=80,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×60×80=2400.
点评 本题主要考查菱形的性质,掌握菱形的对角线互相垂直平分、四边相等是解题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.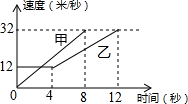 如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
 如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图,是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )| A. | 乙前4秒行驶的路程为48米 | |
| B. | 在0到8秒内甲的速度每秒增加4米 | |
| C. | 在4至8秒内甲的速度都大于乙的速度 | |
| D. | 两车到第3秒时行驶的路程相等 |
14.在四边形ABCD中,AC⊥BD,点E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
4.下列不等式中一定成立的是( )
| A. | 5a>4a | B. | -a>-2a | C. | a+2<a+3 | D. | $\frac{2}{a}$<$\frac{3}{a}$ |
8.在下列四项调查中,方式正确的是( )
| A. | 了解本市中学生每天学习所用的时间,采用全面调查的方式 | |
| B. | 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 | |
| C. | 了解某市每天的流动人口数,采用全面调查的方式 | |
| D. | 了解全市中学生的视力情况,采用抽样调查的方式 |
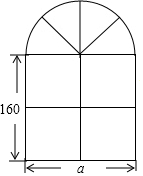 学习了整式的知识,请你解答下列实际问题:(图中长度单位:cm)窗户的形状如图所示,其上半部分是半圆形,下部是形状大小相同的四个小长方形.
学习了整式的知识,请你解答下列实际问题:(图中长度单位:cm)窗户的形状如图所示,其上半部分是半圆形,下部是形状大小相同的四个小长方形.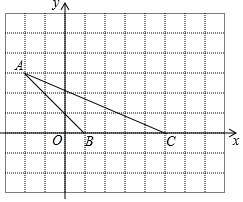 如图所示,小方格边长为1个单位,
如图所示,小方格边长为1个单位,