题目内容
1. 如图,在△ABC中,点D在AC上,且BD=BC=AD,∠DBC=20度,求∠A、∠C,∠ABC的度数.
如图,在△ABC中,点D在AC上,且BD=BC=AD,∠DBC=20度,求∠A、∠C,∠ABC的度数.
分析 根据等腰三角形性质和三角形的内角和可求∠BDC的度数,运用三角形的外角的性质求解.
解答 解:∵BD=BC,∠DBC=20°,
∴∠BDC=$\frac{180°-20°}{2}$=80°,
∵AD=BD,
∴∠A=∠ABD,
∵∠BDC=∠A+∠ABD,
∴∠A=$\frac{1}{2}$∠BDC=40°,
∴∠ABC=∠C=70°.
点评 此题考查等腰三角形的性质和三角形内角和定理,三角形外角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
11.已知锐角α的余弦值是0.6,则锐角α的正切值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
13. 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
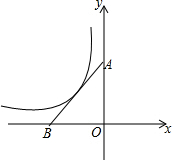 如图,在平面直角坐标系中,点A,B分别在y轴的正半轴和x轴的负半轴上,Rt△AOB的面积是4,若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点,则k的值是-2.
如图,在平面直角坐标系中,点A,B分别在y轴的正半轴和x轴的负半轴上,Rt△AOB的面积是4,若反比例函数y=$\frac{k}{x}$在第二象限内的图象经过斜边AB的中点,则k的值是-2. 如图,点A、C、B、D在⊙O上,∠AOB=60°,OC平分∠AOB,则∠CDB的度数是15°.
如图,点A、C、B、D在⊙O上,∠AOB=60°,OC平分∠AOB,则∠CDB的度数是15°.