题目内容
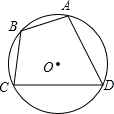
11. 如图,点A、C、B、D在⊙O上,∠AOB=60°,OC平分∠AOB,则∠CDB的度数是15°.
如图,点A、C、B、D在⊙O上,∠AOB=60°,OC平分∠AOB,则∠CDB的度数是15°.
分析 由∠AOB=60°,OC平分∠AOB,可得∠BOC=30°,根据同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得结论.
解答 解:∵∠AOB=60°,OC平分∠AOB,
∴∠BOC=30°,
点A、B、C、D在⊙O上,
∴∠CDB=$\frac{1}{2}$∠BOC=15°.
故答案为15°.
点评 此题考查了圆周角定理.此题比较简单,熟练掌握圆周角定理是解题的关键.

练习册系列答案
相关题目
3.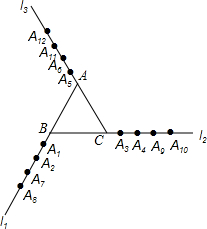 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )| A. | 在直线l1上 | B. | 在直线l2上 | ||
| C. | 在直线l3上 | D. | 不能确定在哪条直线上 |
20. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )| A. | 2π | B. | 4π | C. | 5π | D. | 6π |
1.(-3)100×($-\frac{1}{3}$)100等于( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | 1 |
 如图,在△ABC中,点D在AC上,且BD=BC=AD,∠DBC=20度,求∠A、∠C,∠ABC的度数.
如图,在△ABC中,点D在AC上,且BD=BC=AD,∠DBC=20度,求∠A、∠C,∠ABC的度数. 如图,AB∥DE,∠1=∠2=60°,B、E、C在同一条直线上,∠CED=2∠AEB,求∠C的度数.
如图,AB∥DE,∠1=∠2=60°,B、E、C在同一条直线上,∠CED=2∠AEB,求∠C的度数.
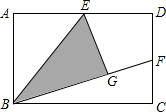 (1)如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.