题目内容
11.已知锐角α的余弦值是0.6,则锐角α的正切值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
分析 根据同角三角函数关系:sin2α+cos2α=1,tanα=$\frac{sinα}{cosα}$,可得答案.
解答 解:由α是锐角,且cosα的值为0.6,得
sinα=$\sqrt{1-co{s}^{2}α}$=$\sqrt{1-\frac{9}{25}}$=$\frac{4}{5}$,
tanα=$\frac{sinα}{cosα}$=$\frac{\frac{4}{5}}{0.6}$=$\frac{4}{3}$.
故选C.
点评 本题考查了同角三角函数关系,利用sin2α+cos2α=1,tanα=$\frac{sinα}{cosα}$是解题关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.由下表的对应值知,一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的一个根的十分位上的数字是1.
| x | 1.1 | 1.2 | 1.3 | 1.4 |
| ax2+bx+c | -0.59 | 0.84 | 2.29 | 3.76 |
18.在?ABCD中,∠A:∠B=2:1,则∠D为( )
| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
20.使用去括号方法和加法交换律后,8-(-3)+(-5)+(-7)等于( )
| A. | 8-3+5-7 | B. | 3+8-7-5 | C. | -5-7-3+8 | D. | 8+3-5+7 |
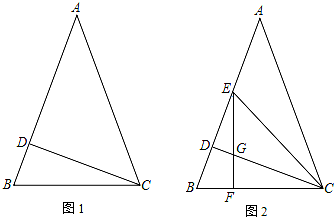
 如图,在△ABC中,点D在AC上,且BD=BC=AD,∠DBC=20度,求∠A、∠C,∠ABC的度数.
如图,在△ABC中,点D在AC上,且BD=BC=AD,∠DBC=20度,求∠A、∠C,∠ABC的度数.