题目内容
15.如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O、A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C7,若点P(13,m)在第7段抛物线C7上,则m=1.
分析 将这段抛物线C1通过配方法求出顶点坐标及抛物线与x轴的交点,由旋转的性质可以知道C1与C2的顶点到x轴的距离相等,且OA1=A1A2,照此类推可以推导知道点P(13,m)为抛物线C7的顶点,从而得到结果.
解答 解:∵y=-x(x-2)(0≤x≤2),
∴配方可得y=-(x-1)2+1(0≤x≤2),
∴顶点坐标为(1,1),
∴A1坐标为(2,0).
∵C2由C1旋转得到,
∴OA1=A1A2,即C2顶点坐标为(3,-1),A2(4,0);
照此类推可得,C3顶点坐标为(5,1),A3(6,0);
C4顶点坐标为(7,-1),A4(8,0);
C5顶点坐标为(9,1),A5(10,0);
C6顶点坐标为(11,-1),A6(12,0);
C7顶点坐标为(13,1),A7(14,0);
∴m=1.
故答案为1.
点评 本题考查了二次函数图象与几何变换及旋转的性质,解题的关键是求出抛物线的顶点坐标.

练习册系列答案
相关题目
10.对于正比例函数y=2x,下列判断正确的是( )
| A. | 自变量x的值毎增加1,函数y的值增加2 | |
| B. | 自变量x的值毎增加1,函数y的值减少2 | |
| C. | 自变量x的值毎增加1,函数y的值增加$\frac{1}{2}$ | |
| D. | 自变量x的值毎增加1,函数y的值减少$\frac{1}{2}$ |
20.在下列各组中,哪个选项表示互为相反意义的是( )
| A. | 足球比赛胜5场与负6场 | B. | 向东走3千米,再向前走3千米 | ||
| C. | 增产10吨粮食与减产-10吨粮食 | D. | 下降的反义词是上升 |
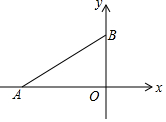 如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).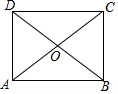 如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.
如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.