题目内容
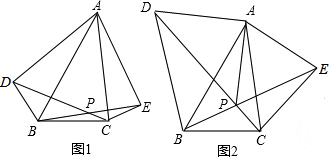
1.已知△ABC是直角三角形,∠ABC=90°,在△ABC外作直角三角形ACE,∠ACE=90°(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;
(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD,∠EAC=45°,AE=$\sqrt{10}$,求四边形ABDE的面积.

分析 (1)由Rt△ACB≌Rt△ACM,推出BC=CM由AB=AM,推出BM⊥AC,由∠ACE=90°,推出AC⊥CE,推出BM∥CE.
(2)如图2中,作EF⊥BD于F,首先求出AC、CE、AB、BC、CD的长,再证明△ABC≌△CFE,推出BC=EF=1,根据S四边形ABDE=S△ABC+S△ACE+S△CDE计算即可.
解答 (1)证明:如图1中,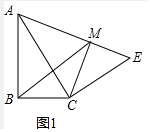
∵CM⊥AE,
∴∠ABC=∠AMC=90°,
在Rt△ACB和Rt△ACM中,
$\left\{\begin{array}{l}{AC=AC}\\{AB=AM}\end{array}\right.$,
∴Rt△ACB≌Rt△ACM,
∴BC=CM,∵AB=AM,
∴BM⊥AC,
∵∠ACE=90°,
∴AC⊥CE,
∴BM∥CE.
(2)解:如图2中,作EF⊥BD于F.
∵∠ACE=90°,∠EAC=45°,
∴∠CAE=∠CEA=45°,
∴CA=CE,∵AE=$\sqrt{10}$,
∴AC=CE=$\sqrt{5}$,
在Rt△ABC中,∵AB=2BC,
∴BC2+4BC2=5,
∴BC=1,AB=2,
∴CB=CD=1,
∵∠ACB+∠BAC=90°,∠ACB+∠ECF=90°,
∴∠BAC=∠ECF,
在△ABC和△CFE中,
$\left\{\begin{array}{l}{∠B=∠F=90°}\\{∠CAB=∠ECF}\\{AC=CE}\end{array}\right.$,
∴△ABC≌△CFE,
∴BC=EF=1,
∴S四边形ABDE=S△ABC+S△ACE+S△CDE=$\frac{1}{2}$×1×2+$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$+$\frac{1}{2}$×1×1=4.
点评 本题考查全等三角形的判定和性质、线段的垂直平分线的判定、平行线的判定、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案 如图,点A,B,C,D顺次在直线l上,已知AC=10,BD=16,AD=20,则BC长为( )
如图,点A,B,C,D顺次在直线l上,已知AC=10,BD=16,AD=20,则BC长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
| A. | a2•a5=a10 | B. | $\sqrt{a+b}$=$\sqrt{a}$+$\sqrt{b}$ | C. | $\sqrt{{a}^{2}}$=a | D. | (-a3)6=a18 |
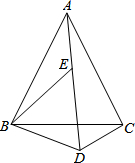 如图,已知△ABC和△BDE均为等边三角形,求证:BD+CD=AD.
如图,已知△ABC和△BDE均为等边三角形,求证:BD+CD=AD.