题目内容
6.已知△ABC中,分别以AB,AC为边在△ABC外侧作△ABD和△ACE,使AB=AD,AC=AE,且∠BAD=∠EAC,BE,CD交于点P.(1)如图1,求证:CD=BE;
(2)如图2,∠BAD=60°,设AB,PD交于点F,若∠PAF=30°,PF=1,求DF的长.
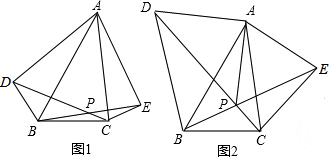
分析 (1)由SAS证明△ACD≌△AEB,得出对应边相等即可;
(2)在PD上截取PM=PA,连接AM,同(1)得:△ACD≌△AEB,得出∠ADC=∠ABE,得出A、D、B、P四点共圆,由圆周角定理得出∠APD=∠ABD,证出△ABD是等边三角形,得出∠ABD=60°,即可知∠APD=60°,结合∠PAF=30°得∠AFP=∠AFD=90°,再由AF=APtan∠APF=$\sqrt{3}$可得DF=AFtan∠DAF=3.
解答 解:(1)∵∠BAD=∠EAC,
∴∠DAC=∠BAE,
在△ACD和△AEB中,
∵$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ACD≌△AEB(SAS),
∴CD=BE;
(2)在PD上截取PM=PA,连接AM,如图所示: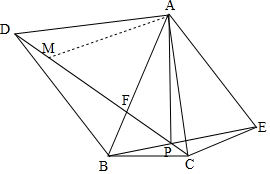
由(1)得:△ACD≌△AEB,
∴∠ADC=∠ABE,
∴A、D、B、P四点共圆,
∴∠APD=∠ABD,
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠APD=60°,
∵∠PAF=30°,
∴∠AFP=∠AFD=90°,
在Rt△APF中,AF=APtan∠APF=$\sqrt{3}$,
在Rt△ADF中,DF=AFtan∠DAF=$\sqrt{3}$×$\sqrt{3}$=3.
点评 本题是三角形综合题目,考查了全等三角形的判定与性质、等边三角形的判定与性质、四点共圆、圆周角定理等知识,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.边长为a,b的长方形周长为12,面积为10,则a2b+ab2的值为( )
| A. | 120 | B. | 60 | C. | 80 | D. | 40 |
18.下列判断正确的是( )
| A. | -$\frac{3}{5}$<-$\frac{4}{7}$ | B. | x-1是有理数,它的倒数是$\frac{1}{x-1}$ | ||
| C. | 若|a|=|b|,则a=b | D. | 若|a|=-a,则a<0 |
15. 如图所示的几何体,从左面看到的形状图是( )
如图所示的几何体,从左面看到的形状图是( )
 如图所示的几何体,从左面看到的形状图是( )
如图所示的几何体,从左面看到的形状图是( )| A. |  | B. |  | C. |  | D. |  |
16.下列英文字母既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△BCD中,BC=4,BD=5,
如图,在△BCD中,BC=4,BD=5,