题目内容
15.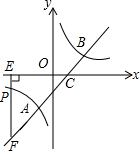 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m).
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m).(1)反比例函数的解析式为y=$\frac{2}{x}$,直线y=x-1在双曲线y=$\frac{k}{x}$上方时x的取值范围是-1<x<0或x>2;
(2)若点P(n,-1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
分析 (1)直接把A(-1,m)代入直线y=x-1求出m的值,故得出A点坐标,代入反比例函数的解析式可得出k的值,进而得出B点坐标,利用函数图象可求出x的取值范围;
(2)先把P点坐标代入反比例函数求出n的值,再求出C点坐标,利用三角形的面积公式即可得出结论.
解答 解:(1)∵A(-1,m),
∴m=-1-1=-2,
∴A(-1,-2),
∴k=(-1)×(-2)=2,
∴反比例函数的解析式为y=$\frac{2}{x}$.
联立一次函数与反比例函数的解析式得$\left\{\begin{array}{l}y=x-1\\ y=\frac{2}{x}\end{array}\right.$,解得$\left\{\begin{array}{l}x=-1\\ y=-2\end{array}\right.$或$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,
∴B(2,1).
由函数图象可知,当-1<x<0或x>2时,直线y=x-1在双曲线y=$\frac{k}{x}$上方.
故答案为:y=$\frac{2}{x}$,-1<x<0或x>2;
(2)∵点P(n,-1)是反比例函数图象上一点,
∴-1=$\frac{2}{n}$,解得n=-2,
∴E(-2,0),F(-2,-3).
∵直线y=x-1中,当x=0时,x=1,
∴C(1,0),
∴CE=|-2-1|=3,
∴S△CEF=$\frac{1}{2}$CE•EF=$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 本题考查的是反比例函数与一次函数的交点问题,能利用函数图象直接得出不等式的值范围是解答此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
5.下列说法正确的是( )
| A. | “抛掷一枚硬币,正面向上”是不可能事件 | |
| B. | 一组数据2,3,4,5,5,2,4,2,2的中位数是3 | |
| C. | 若甲、乙两组数据的方差分别为S甲2=1.2、S乙2=2.3,则乙组数据比甲组数据稳定 | |
| D. | 掷一枚骰子,偶数点向上的概率为$\frac{1}{3}$ |
3.用反证法证明真命题“四边形中至少有一个角不小于90°”时,应假设( )
| A. | 四边形中没有一个角不小于90° | B. | 四边形中至少有两个角不小于90° | ||
| C. | 四边形中四个角都不小于90° | D. | 四边形中至多有一个角不小于90° |
7. 如图,同位角是( )
如图,同位角是( )
 如图,同位角是( )
如图,同位角是( )| A. | ∠1和∠2 | B. | ∠3和∠4 | C. | ∠2和∠4 | D. | ∠1和∠4 |
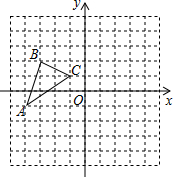 如图所示,在平面直角坐标系中,平移三角形ABC,使A的对应点A1的坐标为(1,-3),B的对应点为B1,C的对应点为C1.
如图所示,在平面直角坐标系中,平移三角形ABC,使A的对应点A1的坐标为(1,-3),B的对应点为B1,C的对应点为C1. 如图,a∥b,BC平分∠ABD,DE⊥BC,若∠1=56°,求∠2的度数.
如图,a∥b,BC平分∠ABD,DE⊥BC,若∠1=56°,求∠2的度数.