题目内容
6．已知分式$\frac{x-3}{{{x^2}-5x+a}}$，当a＜6时，使分式无意义的x的值共有2个．分析 先根据分式无意义的条件列出关于x的不等式，再根据a＜6即可得出结论．
解答 解：由题意得：x2-5x+a=0，
∵当x2-5x+a=0时，△=52-4a=25-4a，
∵a＜6，
∴△=25-4a＞0，
∴当a＜6时，分式方程有两个不相等的实数根，即使分式无意义的x的值共有2个．
点评 本题考查的是分式有意义的条件，熟知分式有意义的条件是分母不等于零是解答此题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
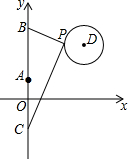如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1-t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是$\sqrt{13}$-1．
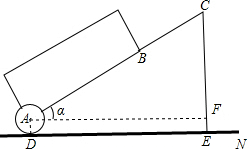拉杆箱是人们出行的必需品，采用拉杆箱可以让我们的出行更轻松，如图，已知某种拉杆箱箱体长AB=50cm，拉杆最大伸长距离BC=40cm，点A到地面的距离AD=8cm，拉杆箱与水平面的夹角α的度数为35°．（提示：sin35°≈0.57，cos35°≈0.82）．
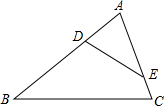如图，在△ABC中，点D在AB边上，点E在AC边上，且∠AED=∠B，若AE=3，EC=1，AD=2．求AB的长．
如图，点O是⊙O的圆心，点A、B、C在⊙O上，∠AOB=42°，则∠ACB的度数是21°．