题目内容
6.用边长为1cm的小正方形搭如图所示的塔状图形,第1次图形的周长为4cm,第2次图形的周长为8cm.按照这种方式搭下去,第n此所搭图形的周长是4ncm.(用含n的代数式表示)
分析 解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
解答 解:第一次:1个小正方形的时候,周长等于1个正方形的周长,是1×4=4;
第二次:3个小正方形的时候,一共有4条边被遮挡,相当于少了1个小正方形的周长,所搭图形的周长为2个小正方形的周长,是2×4=8;
第三次:6个小正方形的时候,一共有12条边被遮挡,相当于少了3个小正方形的周长,所搭图形的周长为3个小正方形的周长,是3×4=12;
….
找到规律,
第n次:第几次搭建的图形的周长就相当于几个小正方形的周长是n×4=4n.
所以第n个图形的周长为4n.
故答案为:4n.
点评 考查了图形的变化类问题,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的以及与第一个图形的相互联系,探寻其规律.

练习册系列答案
相关题目
1.某娱乐场所组织一个翻奖牌游戏,数字的背面写有祝福语或奖金数.游戏规则是:每次翻动正面一个数字,看看背面对应的内容,就可以知道是得奖还是得到温馨祝福.请你回答下列问题:
(1)翻到奖金50元的概率是多少?
(2)翻到祝福身体健康的概率是多少?
(3)翻不到奖金的概率是多少?
正面
背面.
(1)翻到奖金50元的概率是多少?
(2)翻到祝福身体健康的概率是多少?
(3)翻不到奖金的概率是多少?
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 祝你 开心 | 奖金100元 | 学习 进步 |
| 身体 健康 | 奖金 50元 | 身体 健康 |
| 奖金 10元 | 生活 愉快 | 奖金 10元 |
 如图,折线ABC是某市在2012年乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象,观察图象回答,乘客在乘车里程超过3千米时,每多行驶1km,要再付费1.4元.
如图,折线ABC是某市在2012年乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象,观察图象回答,乘客在乘车里程超过3千米时,每多行驶1km,要再付费1.4元.
 如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.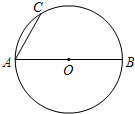 如图,AB是⊙O的直径,AC是弦.
如图,AB是⊙O的直径,AC是弦.