Question

18．（1）如图1，AB∥CD，CE平分∠ACD，AE平分∠BAC，请说明∠E=90°的理由．
（2）如图2，AB∥CD，∠E=90°保持不变，使∠MCE=∠ECD，请直接写出∠BAE与∠MCD的数量关系∠BAE+$\frac{1}{2}$∠MCD=90°
（3）如图3，AB∥CD，P为线段AC上一定点，点Q为直线CD上一动点，（点C除外）问：
∠CPQ+∠CQP与∠BAC有何数量关系？∠CPQ+∠CQP=∠BAC（直接写出结果）．

Answer 1

分析 （1）根据两直线平行，同旁内角互补可得∠BAC+∠ACD=180°，再根据角平分线的定义求出∠EAC+∠ECA=90°，然后求出∠E=90°；
（2）设延长AE交DG于点F，根据平行线的性质可得∠BAE=∠AFC，结合直角的知识可得∠AFC+∠ECD=90°．再结合∠MCE=∠ECD得到结论；
（3）根据平行线的性质得到∠BAC+∠DCP=180°，再结合三角形内角和为180°即可得到结论．

解答 解（1）∵AB∥CD，
∴∠BAC+∠ACD=180°，
∵AE平分∠BAC，CE平分∠ACD，
∴∠EAC+∠ECA=$\frac{1}{2}$（∠BAC+∠ACD）=90°，
∴∠E=90°；
（2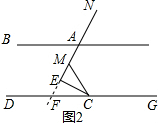）∠BAE+$\frac{1}{2}$∠MCD=90°，
证明：∵延长AE交DG于点F，
∵AB∥CD，
∴∠BAE=∠AFC．
∵∠AEC=90°，
∴∠CEF=90°，
∴∠AFC+∠ECD=90°．
∵∠MCE=∠ECD，
∴∠BAE+$\frac{1}{2}$∠MCD=90°，
故答案为∠BAE+$\frac{1}{2}$∠MCD=90°；
（3）∵AB∥CD，
∴∠BAC+∠DCP=180°，
∵∠CPQ+∠CQP+∠DCP=180°，
∴∠CPQ+∠CQP=∠BAC．

点评 本题考查的是平行线的性质以及垂线的知识，解题要掌握两直线平行，同旁内角互补，根据题意作出辅助线是解答（2）题的关键．