题目内容
14.已知二次函数y=x2-(m2-4)x+2m2-12(1)求证:不论m取何实数,它的图象都过一定点,并求出该定点的坐标;
(2)m取何实数时,它的图象与x轴的两个交点的距离最小?求出这个最小值.
分析 (1)令二次函数解析式中y=0,得到关于x的一元二次方程,解方程即可;
(2)由(1)知图象与x轴的两个交点,让|x1-x2|=0即可.
解答 解:(1)令y=0,得:0=x2-(m2-4)x+2m2-12,
则[x-(m2-6)](x-2)=0,
解得:x1=m2-6,x2=2
所以不论m取何实数,它的图象都过一定点,该定点的坐标为(2,0);
(2)由(1)知抛物线与x轴的两交点坐标为(m2-6,0),(2,0),
∴|x1-x2|=|m2-8|
要使抛物线的图象与x轴的两个交点的距离最小,即|m2-8|=0,
解得:m=±$2\sqrt{2}$,此时最小值为0.
点评 本题考查了抛物线与x轴的交点,二次函数与一元二次方程的关系,求出抛物线与x轴的两交点坐标是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立,则a,b,c的值分别为( )
| A. | 3,-7,-1 | B. | -3,7,-1 | C. | 3,7,-1 | D. | -3,-7,1 |
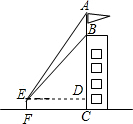 如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.