题目内容
4.先化简($\frac{a}{a^2-3a}$-$\frac{2a}{a^2-9}$)÷$\frac{a-2}{a^2+6a+9}$,然后从不等式组$\left\{\begin{array}{l}{2a+3>a-1}\\{a+8≥4a-1}\end{array}\right.$的解集中选取一个你认为合适的整数作为a的值代入求值.分析 先化简,再求出a的取值,找a值代入求解即可.
解答 解:($\frac{a}{a^2-3a}$-$\frac{2a}{a^2-9}$)÷$\frac{a-2}{a^2+6a+9}$=[$\frac{a}{a(a-3)}$-$\frac{2a}{(a+3)(a-3)}$]•$\frac{(a+3)^{2}}{a-2}$=-$\frac{a+3}{a-2}$,
解不等式组$\left\{\begin{array}{l}{2a+3>a-1}\\{a+8≥4a-1}\end{array}\right.$得,-4≤a≤3,
当a=1时,原式=-$\frac{4}{-1}$=4.
点评 本题主要考查了分式的化简求值及一元一次不等式组的整数解,解题的关键是正确的化简.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12.下列运算中,正确的是( )
| A. | (-2)0=1 | B. | $\root{3}{-9}$=-3 | C. | $\sqrt{4}$=±2 | D. | 2-1=-2 |
9.一次函数y=5x+2的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.△ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
| A. | 4 | B. | 4或5 | C. | 5或6 | D. | 6 |
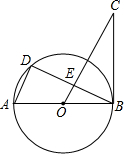 如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.
如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.