题目内容
19.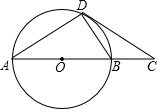 如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )
如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 连接OD,由CD是⊙O的切线,得到OD⊥CD,根据三角形的内角和和等腰三角形的性质得到∠A=∠ADO=30°,推出∠A=∠C,根据等腰三角形的判定得到AD=CD;故②正确;连接BD,推出△DOB是等边三角形,得到BD=OB,∠ODB=60°,求得∠BDC=∠C=30°,根据等腰三角形的判定得到BD=BC,故①正确;由于OB=BC=OA=$\frac{1}{2}$AB,得到AB=2BC,故③正确;根据直角三角形的性质得到OD=$\frac{\sqrt{3}}{3}$CD,于是得到AC=3OD=$\sqrt{3}$CD,故④正确.
解答 解:连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∴∠DOC=60°,
∵OA=OD,
∴∠A=∠ADO=30°,
∴∠A=∠C,
∴AD=CD;故②正确;
连接BD,
∵OD=OB,
∴△DOB是等边三角形,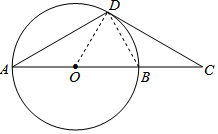
∴BD=OB,∠ODB=60°,
∴∠BDC=∠C=30°,
∴BD=BC,故①正确;
∴OB=BC=OA=$\frac{1}{2}$AB,
∴AB=2BC,故③正确;
∵∠C=30°,
∴OD=$\frac{\sqrt{3}}{3}$CD,
∴AC=3OD=$\sqrt{3}$CD,故④正确;
故选A.
点评 此题考查了切线的性质、等腰三角形的性质以及含30°的直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
9.已知|a|=3,b2=16,且|a+b|≠a+b,则代数式a-b的值为( )
| A. | 1或7 | B. | 1或-7 | C. | -1或-7 | D. | ±1或±7 |
14.下列计算错误的是( )
| A. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ | B. | ($\sqrt{2}$-1)2016($\sqrt{2}$+1)2016=1 | ||
| C. | $\root{3}{(-8)^{3}}$=-8 | D. | 3$\sqrt{2}$-$\sqrt{2}$=3 |
 如图:求作一点P,使PM=PN,并且使点P到∠AOB的两边的距离相等.
如图:求作一点P,使PM=PN,并且使点P到∠AOB的两边的距离相等.