题目内容
10．甲乙两同学用一副扑克牌中牌面数字分别是3，4，5，6的4张牌做抽数字游戏，游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，抽出的牌不放回，然后将剩下的牌洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数，若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请利用树状图或列表法说明理由．分析 游戏是否公平，关键要看是否游戏双方赢的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
解答 解：这个游戏不公平，游戏所有可能出现的结果如下表：
表中共有12种等可能结果，小于45的两位数共有4种，
∴P（甲获胜）=$\frac{4}{12}=\frac{1}{3}$，P（乙获胜）=$1-\frac{1}{3}=\frac{2}{3}$，
∵$\frac{1}{3}$≠$\frac{2}{3}$，
∴这个游戏不公平．
点评 本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
20．下面结论中正确的是（ ）
| A． | $sin{60°}=\frac{1}{2}$ | B． | $tan{60°}=\sqrt{3}$ | C． | $sin{45°}=\frac{{\sqrt{3}}}{2}$ | D． | $cos{30°}=\frac{1}{2}$ |
19．
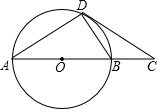如图，AD是⊙O的弦，过点D作⊙O的切线交直径AB的延长线于点C，且∠C=30°．给出四个结论：①BC=BD；②AD=CD；③AB=2BC；④AC=$\sqrt{3}$CD，其中正确的结论有（ ）
如图，AD是⊙O的弦，过点D作⊙O的切线交直径AB的延长线于点C，且∠C=30°．给出四个结论：①BC=BD；②AD=CD；③AB=2BC；④AC=$\sqrt{3}$CD，其中正确的结论有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
20．已知点A（a，1）与点B（5，b）关于原点对称，则a、b值分别是（ ）
| A． | a=1，b=5 | B． | a=5，b=1 | C． | a=-5，b=1 | D． | a=-5，b=-1 |