题目内容
11.计算(1)(-3ab-1)2•(a-2b2)-3
(2)$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$).
分析 (1)原式利用幂的乘方与积的乘方运算法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)(-3ab-1)2•(a-2b2)-3
=9a2b-2•a6b-6
=9a8b-8
=$\frac{{9{a^8}}}{b^8}$;
(2)$\frac{a-b}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$)
=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$.
点评 此题考查了分式的混合运算,以及负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.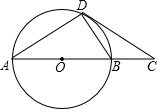 如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )
如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )
 如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )
如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
20.已知点A(a,1)与点B(5,b)关于原点对称,则a、b值分别是( )
| A. | a=1,b=5 | B. | a=5,b=1 | C. | a=-5,b=1 | D. | a=-5,b=-1 |
 如图,用吸管吸易拉罐内的饮料时,吸管与易拉罐的上、下底面所形成的角分别是∠1和∠2,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)
如图,用吸管吸易拉罐内的饮料时,吸管与易拉罐的上、下底面所形成的角分别是∠1和∠2,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行) 如图所示的几何体是由一些小正方体组成的,那么从左边看它的图形是( )
如图所示的几何体是由一些小正方体组成的,那么从左边看它的图形是( )


