题目内容
9.已知|a|=3,b2=16,且|a+b|≠a+b,则代数式a-b的值为( )| A. | 1或7 | B. | 1或-7 | C. | -1或-7 | D. | ±1或±7 |
分析 首先根据|a|=3,可得a=±3;再根据b2=16,可得b=±4;然后根据|a+b|≠a+b,可得a+b<0,据此求出a、b的值各是多少,即可求出代数式a-b的值为多少.
解答 解:∵|a|=3,
∴a=±3;
∵b2=16,
∴b=±4;
∵|a+b|≠a+b,
∴a+b<0,
∴a=3,b=-4或a=-3,b=-4,
(1)a=3,b=-4时,
a-b=3-(-4)=7;
(2)a=-3,b=-4时,
a-b=-3-(-4)=1;
∴代数式a-b的值为1或7.
故选:A.
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.

练习册系列答案
相关题目
20.下面结论中正确的是( )
| A. | $sin{60°}=\frac{1}{2}$ | B. | $tan{60°}=\sqrt{3}$ | C. | $sin{45°}=\frac{{\sqrt{3}}}{2}$ | D. | $cos{30°}=\frac{1}{2}$ |
14.下列各式中,不能用平方差公式计算的是( )
| A. | (4x-3y)(-3y-4x) | B. | (2x2-y2)(2x2+y2) | C. | (a+b)(-b+a) | D. | (-x+y)(x-y) |
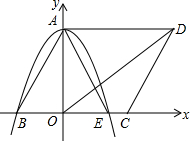 如图,在平面直角坐标系中,四边形ABCD是平行四边形,线段AD=6,二次函数y=-$\frac{1}{2}$x2-$\frac{1}{6}$x+4与y轴交于A点,与x轴分别交于B点、E点(B点在E点的左侧)
如图,在平面直角坐标系中,四边形ABCD是平行四边形,线段AD=6,二次函数y=-$\frac{1}{2}$x2-$\frac{1}{6}$x+4与y轴交于A点,与x轴分别交于B点、E点(B点在E点的左侧) 根据题意结合图形填空:如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.将过程补充完整.
根据题意结合图形填空:如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.试说明:AC∥DF.将过程补充完整.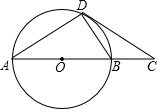 如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )
如图,AD是⊙O的弦,过点D作⊙O的切线交直径AB的延长线于点C,且∠C=30°.给出四个结论:①BC=BD;②AD=CD;③AB=2BC;④AC=$\sqrt{3}$CD,其中正确的结论有( )