题目内容
用边长相等的黑色正三角形与白色正六边形镶嵌图案，按图①②③所示的规律依次下去，则第n个图案中，所包含的黑色正三角形和白色正六边形的个数总和是 ．
考点：规律型：图形的变化类
专题：
分析：观察图形可知图形①的黑色正三角形=4×1=4，白色正六边形的个数=3个，图形②的黑色正三角形=4×2=8，白色正六边形的个数=5个，图形③的黑色正三角形=4×3=12，白色正六边形的个数=7个，…依此类推，图形n的黑色正三角形和白色正六边形的个数总和=4n+2n+1=6n+1个．
解答：解：图形①的黑色正三角形和白色正六边形的个数总和=4×1+3=7个，
图形②的黑色正三角形和白色正六边形的个数总和=4×2+5=13个，
图形③的黑色正三角形和白色正六边形的个数总和=4×3+7=19个，
…
图形n的黑色正三角形和白色正六边形的个数总和=4n+2n+1=6n+1个．
故答案为：6n+1．
图形②的黑色正三角形和白色正六边形的个数总和=4×2+5=13个，
图形③的黑色正三角形和白色正六边形的个数总和=4×3+7=19个，
…
图形n的黑色正三角形和白色正六边形的个数总和=4n+2n+1=6n+1个．
故答案为：6n+1．
点评：此题考查图形的变化规律，从简单情形分析，找出规律解决问题．
练习册系列答案
相关题目
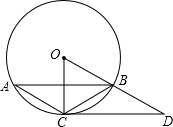如图，已知△ABC内接于⊙O，点D在半径OB的延长线上，∠BCD=∠A=30°．
如图，点A在反比例函数y=
如图，半圆的直径AB=10，弦CD∥AB，且∠CAD=30°，则图中阴影部分的面积为