题目内容
11.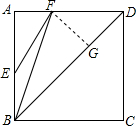 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
分析 首先设正方形ABCD的边长为3,利用正方形的性质和$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$求得EB、AF、AE、FD,进一步利用勾股定理求得FG、BF、EF、BG,利用三边对应成比例求得△AEF∽△BGF,得出结论.
解答 证明:如图,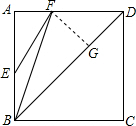
作FG⊥BD于点G,
设正方形ABCD的边长为3,
则AB=AD=3,∠ADB=45°,
∵$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$,
∴EB=1,AF=1,AE=3-1=2,FD=3-1=2,
∴EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{5}$,
BF=$\sqrt{A{B}^{2}+A{F}^{2}}$=$\sqrt{10}$,
FG=$\sqrt{2}$,
BG=$\sqrt{B{F}^{2}-F{G}^{2}}$=2$\sqrt{2}$,
∵$\frac{AF}{FG}$=$\frac{\sqrt{2}}{2}$,$\frac{AE}{BG}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,$\frac{EF}{BF}$=$\frac{\sqrt{5}}{\sqrt{10}}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AF}{FG}$=$\frac{AE}{BG}$=$\frac{EF}{BF}$,
∴△AEF∽△GBF,
∴∠AEF=∠FBD.
点评 此题考查相似三角形的判定与性质,勾股定理,正方形的性质,掌握三角形相似的判定与性质是解决问题的关键.

练习册系列答案
相关题目
2.当x=( )时,|x+6|有最( )值,是( )
| A. | 0,大,0 | B. | 0,小,0 | C. | -6,大,0 | D. | -6,小,0 |
 如图,已知AD是△BAC的角平分线,AD的垂直平分线EF交BC的延长线于点E,试说明:ED2=EC•EB.
如图,已知AD是△BAC的角平分线,AD的垂直平分线EF交BC的延长线于点E,试说明:ED2=EC•EB.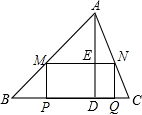 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y. 如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).
如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).