题目内容
6. 如图,已知AD是△BAC的角平分线,AD的垂直平分线EF交BC的延长线于点E,试说明:ED2=EC•EB.
如图,已知AD是△BAC的角平分线,AD的垂直平分线EF交BC的延长线于点E,试说明:ED2=EC•EB.
分析 由FE是AD的垂直平分线得到FA=FD,再根据等边对等角得到∠FAD=∠FDA,而∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,其中由AD是∠BAC的平分线可以得到∠1=∠2,可得∠BAF=∠ACF,再加上公共角∠BFA=∠AFB,可得△BAF∽△ACF,再根据相似三角形的性质可得结论.
解答 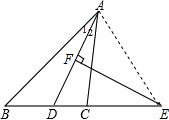 证明:连接AE,
证明:连接AE,
∵AD是∠BAC的平分线,
∴∠1=∠2,
∵FE是AD的垂直平分线,
∴EA=ED(线段垂直平分线上的点到线段两端的距离相等),
∴∠EAD=∠EDA(等边对等角),
∵∠BAE=∠EAD+∠1,∠ACE=∠EDA+∠2,
∴∠BAE=∠ACE,
又∵∠BFA=∠AFB,
∴△BAE∽△ACE,
∴$\frac{AE}{BF}$=$\frac{CE}{AE}$,
∴AE2=BE•CE,
∴DE2=BE•CE.
点评 此题考查了相似三角形的判定和性质,角平分线的性质、线段的垂直平分线性质、相似三角形的判定与性质,关键是证明△BAF∽△ACF.

练习册系列答案
相关题目
19.下列从左到右的变形是因式分解的是( )
| A. | (2x+1)(2x-1)=4x2-1 | B. | a2-3a-4=a(a-3)-4 | C. | 8x5y2=4x3y2•2x2 | D. | m(n-1)-(n-1)=(m-1)(n-1) |
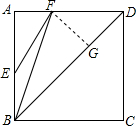 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.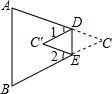 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数. 如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第2016次输出的结果为6.
如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第2016次输出的结果为6.