题目内容
3. 如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).
如图,在一面靠墙的空地上,用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为S(m2).(1)求S与x的函数关系式及自变量的取值范围;
(2)若从设计的美观角度出发,墙的最小利用长度为4m,最大利用长度为8m,此时,围成的花圃最大面积和最小面积分别是多少?
分析 (1)求出S=AB×BC代入即可;
(2)利用4≤24-4x≤8进而解出自变量的取值范围,把解析式化成顶点式,再利用二次函数增减性即可得到答案.
解答 解:(1)设花圃的宽AB为x米,则BC=(24-4x)m,
根据题意得出:S=x(24-4x)=-4x2+24x,(0<x<6);
(2)∵墙的最小利用长度为4m,最大利用长度为8m,
∴4≤24-4x≤8
解得:4≤x≤5,
S=-4x2+24x=-4(x2-6x)=-4(x-3)2+36,
∵4≤x≤5,
∴当x=5m时,S最小值=20平方米,
当x=4m时,S最大值=32 平方米.
点评 本题主要考查对二次函数的最值,二次函数的解析式,解一元二次方程等知识点的理解和掌握,能把实际问题转化成数学问题是解此题的关键.

练习册系列答案
相关题目
12. 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )| A. | 12 | B. | 16 | C. | 24 | D. | 36 |
 如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.
如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.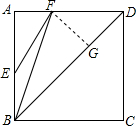 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.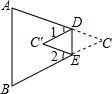 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=30°,求∠2的度数.