题目内容
 如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数.
如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数.考点:圆周角定理
专题:
分析:由三角形外角的性质,易求得∠APC=∠C+∠AQC+∠A,又由圆周角定理,可得∠A=∠C,即可求得∠A与∠C的度数,继而求得∠ADC的度数.
解答:解:∵∠ADC=∠C+∠AQC,∠APC=∠A+∠ADC,
∴∠APC=∠C+∠AQC+∠A,
∵∠A=∠C,∠AQC=36°,∠APC=80°,
∴80°=2∠A+36°,
∴∠A=22°,
∴∠BCD=∠A=22°,∠ADC=∠APC-∠A=58°.
∴∠APC=∠C+∠AQC+∠A,
∵∠A=∠C,∠AQC=36°,∠APC=80°,
∴80°=2∠A+36°,
∴∠A=22°,
∴∠BCD=∠A=22°,∠ADC=∠APC-∠A=58°.
点评:此题考查了圆周角定理与三角形外角的性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图,在⊙O中,OD⊥BC,∠BOD=50°,则∠CAD的度数等于( )
如图,在⊙O中,OD⊥BC,∠BOD=50°,则∠CAD的度数等于( )| A、30° | B、25° |
| C、20° | D、15° |
在2.5,-2.5,0,2这四个数中,最小的一个数是( )
| A、2.5 | B、-2.5 | C、0 | D、2 |
 如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是
如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是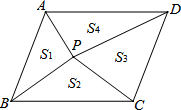 如图,点P是平行四边形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
如图,点P是平行四边形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论: 如图,点D是△ABC的外接圆的弧
如图,点D是△ABC的外接圆的弧
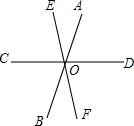 如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.
如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.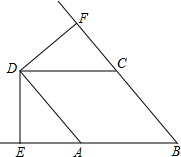 如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形.
如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形.