题目内容
已知a、b、c满足
+
+
=1,则
+
+
的值为多少?
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| a2 |
| b+c |
| b2 |
| c+a |
| c2 |
| a+b |
考点:分式的条件求值
专题:计算题
分析:设a+b+c=d,则有a=d-(b+c),b=d-(a+c),c=d-(a+b),然后把它们代入到所求分式,化简后就可解决问题.
解答:解:设a+b+c=d,则有a=d-(b+c),b=d-(a+c),c=d-(a+b).
∵
+
+
=1,
∴
+
+
=
•a+
•b+
•c
=
•[d-(b+c)]+
•[d-(a+c)]+
•[d-(a+b)]
=
•d-a+
•d-b+
•d-c
=(
+
+
)•d-(a+b+c)
=d-d=0.
∵
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
∴
| a2 |
| b+c |
| b2 |
| c+a |
| c2 |
| a+b |
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
=
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
=
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
=(
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
=d-d=0.
点评:本题考查了求分式的值,有一定的技巧性,而解决本题的关键是把a+b+c看成一个整体,从而把所求分式与条件联系起来.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
一元二次方程x(x-2014)=2014-x的根是( )
| A、-1 | B、2014 |
| C、1和2014 | D、-1和2014 |

 向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大?
向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大? 如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,AE=CF,求证:AB∥CD.
如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,AE=CF,求证:AB∥CD. 如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是
如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是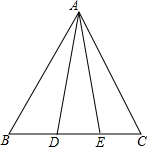 如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程.
如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程.