题目内容
13．正六边形的每一个内角的度数是（ ）| A． | 150° | B． | 120° | C． | 90° | D． | 60° |
分析 多边形的内角和可以表示成（n-2）•180°，因为所给多边形的每个内角均相等，可设这个正六边形的每一个内角的度数为x，故又可表示成6x，列方程可求解．
解答 解：设这个正六边形的每一个内角的度数为x，
则6x=（6-2）•180°，
解得x=120°．
故这个正六边形的每一个内角的度数为120°．
故选B．
点评 本题考查根据多边形的内角和计算公式求多边形的内角的度数，解答时要会根据公式进行正确运算、变形和数据处理．
练习册系列答案
阅读快车系列答案
相关题目
1．
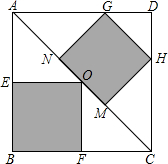如图，正方形ABCD是一块绿化带，其中阴影部分EOFB、GHMN都是正方形的花圃，其中点N、O、M均在AC上，点G、H、F、E分别在AD、DC、CB、BA上，一只自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟落在花圃上的概率为（ ）
如图，正方形ABCD是一块绿化带，其中阴影部分EOFB、GHMN都是正方形的花圃，其中点N、O、M均在AC上，点G、H、F、E分别在AD、DC、CB、BA上，一只自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟落在花圃上的概率为（ ）| A． | $\frac{17}{32}$ | B． | $\frac{1}{2}$ | C． | $\frac{17}{36}$ | D． | $\frac{17}{38}$ |
为有效开发海洋资源，保护海洋权益，我国对南海诸岛进行了全面调查．如图，一测量船在A岛测得B岛在北偏西30°方向，C岛在北偏东15°方向，航行100海里到达B岛，在B岛测得C岛在北偏东45°，求B，C两岛及A，C两岛的距离．（结果保留到整数，$\sqrt{2}$≈1.41，$\sqrt{6}$≈2.45）
5．下列结论中不正确的是（ ）
| A． | 连接两点的线段叫两点之间的距离 | B． | 两点之间，线段最短 | ||
| C． | 等角的余角相等 | D． | 两点确定一条直线 |
2．如果xny4与2xym相乘的结果是2x5y7，那么m和n的值分别是（ ）
| A． | 3，5 | B． | 2，1 | C． | 3，4 | D． | 4，5 |
3．下列计算正确的是（ ）
| A． | （-2a2）3=-8a5 | B． | a3•a2=a5 | C． | 2a2+a2=3a4 | D． | （a-b）2=a2-b2 |