题目内容
5．下列结论中不正确的是（ ）| A． | 连接两点的线段叫两点之间的距离 | B． | 两点之间，线段最短 | ||
| C． | 等角的余角相等 | D． | 两点确定一条直线 |
分析 根据两点之间的距离，等角的余角或补角相等，两点确定一条直线，线段的性质即可判断．
解答 解：A、连接两点的线段的长度叫两点之间的距离，故错误；
B、两点之间，线段最短，故正确；
C、等角的余角相等，故正确；
D、两点确定一条直线，故正确；
故选A．
点评 本题考查了对余角或补角，直线的性质，线段的性质的理解和运用，知识点有：等角的余角或补角相等，两点确定一条直线，两点之间线段最短．
练习册系列答案
相关题目
将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合，当α最小时，点A运动的路径长为$\frac{2π}{3}$．
13．正六边形的每一个内角的度数是（ ）
| A． | 150° | B． | 120° | C． | 90° | D． | 60° |
10．菱形两对角线长分别为24cm和10cm，则菱形的高为（ ） cm．
| A． | 13 | B． | $\frac{240}{13}$ | C． | 120 | D． | $\frac{120}{13}$ |
14．已知方程mx2-2（1-m）x+m=0有实数根，则m满足的条件是（ ）
| A． | m≤$\frac{1}{2}$且m≠0 | B． | m＜$\frac{1}{2}$且m≠0 | C． | m＜$\frac{1}{2}$ | D． | m≤$\frac{1}{2}$ |
15．
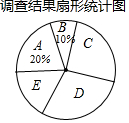2017年全国两会民生话题成为社会焦点．徐州市记者为了了解百姓“两会民生话题”的聚焦点，随机调查了徐州市部分市民，并对调查结果进行整理．绘制了如图所示的不完整的统计图表．
请根据图表中提供的信息解答下列问题：
（1）填空：m=40，n=100．扇形统计图中E组所占的百分比为15%；
（2）徐州市市区人口现有170万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
2017年全国两会民生话题成为社会焦点．徐州市记者为了了解百姓“两会民生话题”的聚焦点，随机调查了徐州市部分市民，并对调查结果进行整理．绘制了如图所示的不完整的统计图表．| 组别 | 焦点话题 | 频数（人数） |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
（1）填空：m=40，n=100．扇形统计图中E组所占的百分比为15%；
（2）徐州市市区人口现有170万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？