题目内容
4.化简:(x-2)•$\sqrt{-\frac{1}{x-2}}$.分析 先确定出x-2的正负,然后依据再将括号外的因式乘到括号内即可.
解答 解:∵-$\frac{1}{x-2}$≥0,
∴x-2<0.
∴原式=-$\sqrt{(x-2)^{2}•(-\frac{1}{x-2})}$=-$\sqrt{2-x}$.
点评 本题主要考查的是二次根式的性质和化简,确定出x-2<0是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
13.正六边形的每一个内角的度数是( )
| A. | 150° | B. | 120° | C. | 90° | D. | 60° |
14.已知方程mx2-2(1-m)x+m=0有实数根,则m满足的条件是( )
| A. | m≤$\frac{1}{2}$且m≠0 | B. | m<$\frac{1}{2}$且m≠0 | C. | m<$\frac{1}{2}$ | D. | m≤$\frac{1}{2}$ |
 将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为$\frac{2π}{3}$.
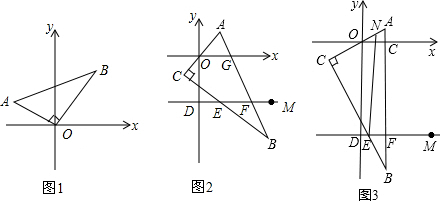
将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为$\frac{2π}{3}$. 金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)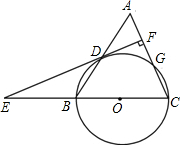 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.