题目内容
18. 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
分析 过B点作BD⊥AC于点D,根据等腰直角三角形的性质求出BD,根据正弦的定义计算即可.
解答 解:过B点作BD⊥AC于点D,
由题意知∠BAC=45°,∠FBA=30°,∠EBC=45°,AB=100海里,∠BAC=45°,
∴△BAD为等腰直角三角形,
∴BD=AD=50$\sqrt{2}$,∠ABD=45°,
∴∠CBD=180°-30°-45°-45°=60°,
∴∠C=30°,
∴在Rt△BCD中,BC=100$\sqrt{2}$≈141(海里),CD=50$\sqrt{6}$,
∴AC=AD+CD=50$\sqrt{2}$+50$\sqrt{6}$≈193(海里),
答:B,C两岛的距离约为141海里,A,C两岛的距离约为193海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
4. 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )| A. | BM=$\frac{1}{2}$AB | B. | AM+BM=AB | C. | AM=BM | D. | AB=2AM |
13.正六边形的每一个内角的度数是( )
| A. | 150° | B. | 120° | C. | 90° | D. | 60° |
10.菱形两对角线长分别为24cm和10cm,则菱形的高为( ) cm.
| A. | 13 | B. | $\frac{240}{13}$ | C. | 120 | D. | $\frac{120}{13}$ |
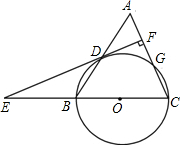 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=44°,∠D=120°,则∠2的度数为38°.
如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=44°,∠D=120°,则∠2的度数为38°.