题目内容
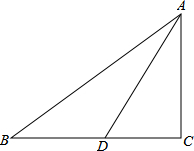 如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=
如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=考点:相似三角形的判定与性质,勾股定理
专题:
分析:如图,作辅助线;证明∠AED=∠ADE=2α,AE=AD;证明AE=3BE(设为3λ),得到AD=AE=3λ;证明9λ2-4=16λ2-16,解得:λ=
,求出AD即可解决问题.
2
| ||
| 7 |
解答: 解:如图,作BD的垂直平分线,交AB于点E,连接DE;
解:如图,作BD的垂直平分线,交AB于点E,连接DE;
则BE=DE(设为λ),BF=DF=1,CF=3;
∴∠B=∠EDB(设为α);
∵∠AED=∠B+∠EDB=2α,∠ADB=3∠B=3α,
∴∠AED=∠ADE=2α,AE=AD;
∵EF⊥BC,AC⊥BC,
∴EF∥AC,
=
=
,
∴AE=3BE(设为3λ),
∴AD=AE=3λ;由勾股定理得:
AC2=AD2-DC2=9λ2-4,
AC2=AB2-BC2=16λ2-16,
∴9λ2-4=16λ2-16,
解得:λ=
,
∴AD=
,
故答案为
.
 解:如图,作BD的垂直平分线,交AB于点E,连接DE;
解:如图,作BD的垂直平分线,交AB于点E,连接DE;则BE=DE(设为λ),BF=DF=1,CF=3;
∴∠B=∠EDB(设为α);
∵∠AED=∠B+∠EDB=2α,∠ADB=3∠B=3α,
∴∠AED=∠ADE=2α,AE=AD;
∵EF⊥BC,AC⊥BC,
∴EF∥AC,
| BE |
| AE |
| BF |
| CF |
| 1 |
| 3 |
∴AE=3BE(设为3λ),
∴AD=AE=3λ;由勾股定理得:
AC2=AD2-DC2=9λ2-4,
AC2=AB2-BC2=16λ2-16,
∴9λ2-4=16λ2-16,
解得:λ=
2
| ||
| 7 |
∴AD=
6
| ||
| 7 |
故答案为
6
| ||
| 7 |
点评:该题主要考查了相似三角形的判定及其性质、勾股定理及其应用问题;解题的关键是作辅助线,构造相似三角形,运用相似三角形的判定及其性质来分析、解答.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 如图,已知OD平分∠AOB,OE平分∠BOD,若
如图,已知OD平分∠AOB,OE平分∠BOD,若| ∠AOC |
| ∠BOC |
| 3 |
| 2 |
| ∠COE |
| ∠BOE |
A、
| ||
B、
| ||
C、
| ||
D、
|
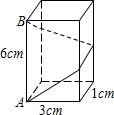 如图,长方体的底面边长为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )
如图,长方体的底面边长为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )| A、12cm | B、11cm |
| C、10cm | D、9cm |
 如图,因为∠1=∠B,所以
如图,因为∠1=∠B,所以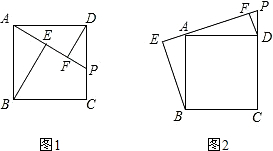
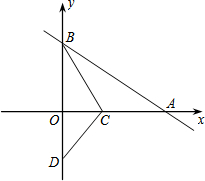 如图:在平面直角坐标系中,直线y=kx+6分别与x轴、y轴交于A、B两点,且OA=8,点C是x轴上一点,如果把△AOB沿着直线BC折叠,那么点A恰好落在y轴负半轴上的点D处.
如图:在平面直角坐标系中,直线y=kx+6分别与x轴、y轴交于A、B两点,且OA=8,点C是x轴上一点,如果把△AOB沿着直线BC折叠,那么点A恰好落在y轴负半轴上的点D处.