题目内容
8.一个直角三角形的两边的长是方程x2-7x+12=0的两个根,则此直角三角形的斜边中线长为2.5或2.分析 解方程x2-7x+12=0求出直角三角形的两边是3,4,这两边可能是两条直角边,根据勾股定理求得斜边,再根据直角三角形斜边上的中线等于斜边的一半求出斜边中线长;也可能是一条直角边和一条斜边,则斜边是4,斜边中线长为2.
解答 解:∵一个直角三角形的两边的长是方程x2-7x+12=0的两个根,
∴直角三角形的两边是3,4,
当这两边都是直角边时,根据勾股定理得其斜边为$\sqrt{{3}^{2}+{4}^{2}}$=5,斜边中线长是2.5;
当这两边一条是直角边和一条斜边时,斜边一定是4,斜边中线长是2.
故答案为2.5或2.
点评 本题考查了直角三角形斜边上的中线的性质,勾股定理,解一元二次方程.注意到分两种情况进行讨论是解决本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.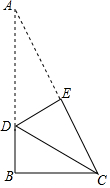 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )| A. | $\frac{7}{8}$ | B. | 1 | C. | $\frac{9}{8}$ | D. | $\frac{2}{3}$ |
3. 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )
 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )| A. | 4 | B. | 6 | C. | 9 | D. | 12 |
13.某中学为筹备校庆活动,准备印刷一批校庆纪念册,该纪念册毎册需要10张同样大小的纸,其中4张为彩页,6张为黑白页,印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为彩页300元/张,黑白页50元/张,印刷费与印数的关系见下表:
求:(1)印刷这批纪念册的制版费为多少元?
(2)若印刷2千册,则共需多少费用?
(3)如果该校希望印数a至少为4千册,总费用为y元,请用含有a的式子表示y?
| 印数a(单位:千册) | 1≤a<5 | a≥5 |
| 彩色(单位:元/张) | 2.2 | 2.0 |
| 黑白(单位:元/张) | 0.7 | 0.6 |
(2)若印刷2千册,则共需多少费用?
(3)如果该校希望印数a至少为4千册,总费用为y元,请用含有a的式子表示y?