题目内容
19. 有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.小东根据学习函数的经验,对函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的自变量x的取值范围是x≠0;
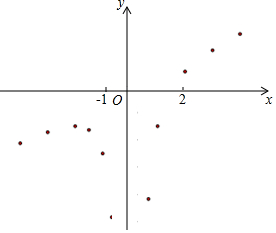
(2)下表是y与x的几组对应值,求m的值;
| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{17}{8}$ | -$\frac{31}{18}$ | -$\frac{3}{2}$ | -$\frac{59}{36}$ | -$\frac{5}{2}$ | -$\frac{29}{6}$ | -$\frac{25}{6}$ | -$\frac{3}{2}$ | $\frac{1}{2}$ | $\frac{23}{18}$ | m | … |
(4)进一步探究发现,该函数图象在第三象限内的最高点的坐标是(-2,-$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)当x>0时,y随x的增大而增大.
分析 (1)由分母不为0,可得出自变量x的取值范围;
(2)将x=4代入函数表达式中,即可求出m值;
(3)连线,画出函数图象;
(4)观察函数图象,找出函数性质.
解答 解:(1)∵x2在分母上,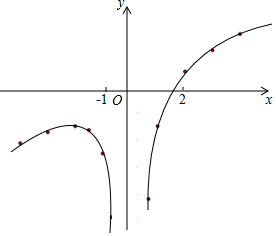
∴x≠0.
故答案为:x≠0.
(2)当x=4时,m=$\frac{1}{2}$x-$\frac{2}{x^2}$=$\frac{1}{2}$×4-$\frac{2}{{4}^{2}}$=$\frac{15}{8}$.
(3)连线,画出函数图象,如图所示.
(4)观察图象,可知:当x>0时,y随x的增大而增大.
故答案为:当x>0时,y随x的增大而增大.
点评 本题考查了分式有意义的条件、二次函数的性质、二次函数的图象以及二次函数的最值,解题的关键是:(1)根据分母不为0,找出x的取值范围;(2)将x=4代入函数关系式求出y值;(3)连点,画出函数图象;(4)根据函数图象,寻找函数的性质.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.如图,把一个矩形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为110°的菱形,剪口与第二次折痕所成角的度数应为( )
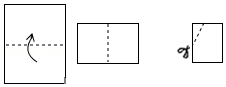

| A. | 70°或20° | B. | 55°或45° | C. | 55°或35° | D. | 55°或65° |
5.图1是某娱乐节目中一个游戏环节的录制现场,场地由等边△ADE和正方形ABCD组成,正方形ABCD两条对角线交于点O,在AD的中点P处放置了一台主摄像机.游戏参与者行进的时间为x,与主摄像机的距离为y,若游戏参与者匀速行进,且表示y与x的函数关系式大致如图2所示,则游戏参与者的行进路线可能是( )
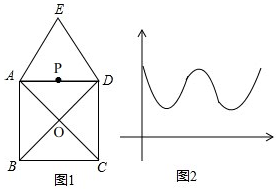

| A. | A→O→D | B. | E→A→C | C. | A→E→D | D. | E→A→B |
4.若|a|<2,且a是整数,那么a为( )
| A. | 2,1,0 | B. | -2,-1,0,1,2 | C. | -1,0,1 | D. | 0,-1,-2 |
11. 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )| A. | SSS | B. | SAS | C. | AAS | D. | HL |
8.分别以2cm、3cm、4cm、5cm的线段为边可构成( )三角形.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9. 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )
 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )| A. | ∠1与∠2是同旁内角 | B. | ∠1与∠3是内错角 | ||
| C. | ∠1与∠5是同位角 | D. | ∠4与∠5互为邻补角 |