题目内容
7.某公司经营甲、乙两种汽车,每辆甲种汽车进价12万元,售价14.5万元,每辆乙种汽车进价8万元,售价10万元,且它们的进价和售价始终不变,现准备购进甲、乙两种汽车共20辆,所用资金不低于195万元,不高于205万元.(1)该公司有哪几种进货方案?
(2)该公司采用哪种进货方案可获得最大利润?最大利润是多少?
(3)若用(2)中所求得的利润再次进货,请你直接写出获得最大利润的进货方案?
分析 (1)关系式为:190≤甲种汽车总进价+乙种汽车总进价≤200,根据此不等关系列不等式组求解即可;
(2)利润=甲种汽车数量×(14.5-12)+乙种汽车数量×(10-8),整理后按(1)中自变量的取值算出最大利润;
(3)用最大利润45万元来进货,用最大利润进货,没有总件数限制,但要考虑尽量把钱用完.分以下五种情况讨论,通过计算比较即可.①全进甲,能购买3辆;②全进乙,能购买5辆;③甲进1辆,同时乙进4辆;④甲进2辆,同时乙进2辆;⑤甲进3辆,同时乙进1辆.
解答 解:(1)设购进甲种汽车x辆,则购进乙种汽车(20-x)辆.
由题意195≤12x+8(20-x)≤205,
解得$\frac{35}{4}$≤x≤$\frac{45}{4}$,
∵x为非负整数,
∴x取9,10,11,
有三种进货方案:
①购甲种汽车9辆,乙种汽车11辆;
②购甲种汽车10辆,乙种汽车10辆;
③购甲种汽车11辆,乙种汽车9辆.
(2)设利润为w元,
则w=x×(14.5-12)+(20-x)×(10-8)=0.5x+40,
因为0.5>0,所以函数w随x的增大而增大,
结合(1)的结果可知,
∴购甲种汽车11辆,乙种汽车9辆时,可获得最大利润,最大利润是45.5万元.
(3)①全进甲,能购买3辆,利润为(14.5-12)×3=7.5万元;
②全进乙,能购买5辆,利润(10-8)×5=10万元;
③甲进1辆,同时乙进4辆,利润(14.5-12)×1+(10-8)×4=10.5万元;
④甲进2辆,同时乙进2辆,利润为2.5×2+2×2=9万元;
⑤甲进3辆,同时乙进1辆,2.5×3+2×1=9.5万元;
∴甲进1辆,同时乙进4辆时,利润最大,最大利润为10.5万元.
点评 本题考查一次函数的应用,不等式的应用解决本题的关键是读懂题意,找到符合题意的不等关系式,及所求量的等量关系.要会用分类的思想来讨论问题并能用不等式的特殊值来求得方案的问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 运输单位 | 运输速度(千米/时) | 运费单价(元/吨•千米) | 装卸费用(元) |
| 汽车货运公司 | 50 | 1.8 | 2500 |
| 火车货运站 | 100 | 1.6 | 4500 |
(2)为减少费用,你认为脐橙基地应该选择哪家运输单位运送脐橙花费少?
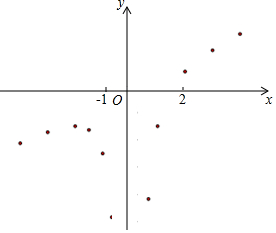 有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.小东根据学习函数的经验,对函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值,求m的值;
| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{17}{8}$ | -$\frac{31}{18}$ | -$\frac{3}{2}$ | -$\frac{59}{36}$ | -$\frac{5}{2}$ | -$\frac{29}{6}$ | -$\frac{25}{6}$ | -$\frac{3}{2}$ | $\frac{1}{2}$ | $\frac{23}{18}$ | m | … |
(4)进一步探究发现,该函数图象在第三象限内的最高点的坐标是(-2,-$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)当x>0时,y随x的增大而增大.
| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |