题目内容
14．用合适的方法解一元二次方程：（x+1）（x-2）=4．分析 整理成一般式后利用因式分解法求解可得．
解答 解：原方程整理可得：x2-x-6=0，
左边因式分解可得（x+2）（x-3）=0，
则x+2=0或x-3=0，
解得：x=-2或x=3．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
相关题目
19．a，b，c为△ABC的三边，化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|，结果是（ ）
| A． | 0 | B． | 2a+2b+2c | C． | 4a | D． | 2b-2c |
2．赣南脐橙名闻天下，我市某脐橙基地请汽车货运公司或火车货运站将40吨脐橙从A地运到B地，已知汽车和火车从A地到B地的运输路程都是s千米，两家运输单位除都要收取运输途中每吨每小时5元的冷藏保鲜费外，其他要收取的费用和有关运输资料由如表列出：
（1）用含s的式子分别表示汽车货运公司和火车货运站运送这批脐橙所要收取的总费用y1（元）和y2（元）；
（2）为减少费用，你认为脐橙基地应该选择哪家运输单位运送脐橙花费少？
| 运输单位 | 运输速度（千米/时） | 运费单价（元/吨•千米） | 装卸费用（元） |
| 汽车货运公司 | 50 | 1.8 | 2500 |
| 火车货运站 | 100 | 1.6 | 4500 |
（2）为减少费用，你认为脐橙基地应该选择哪家运输单位运送脐橙花费少？
9．已知x+y=$\sqrt{2}$，|x|+|y|=5$\sqrt{2}$，则x-y的值为（ ）
| A． | $±2\sqrt{2}$ | B． | $±3\sqrt{2}$ | C． | $±4\sqrt{2}$ | D． | $±5\sqrt{2}$ |
19．
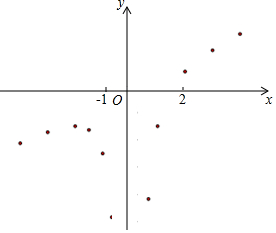有这样一个问题：探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第三象限内的最高点的坐标是（-2，-$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而增大．
有这样一个问题：探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值，求m的值；
| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{17}{8}$ | -$\frac{31}{18}$ | -$\frac{3}{2}$ | -$\frac{59}{36}$ | -$\frac{5}{2}$ | -$\frac{29}{6}$ | -$\frac{25}{6}$ | -$\frac{3}{2}$ | $\frac{1}{2}$ | $\frac{23}{18}$ | m | … |
（4）进一步探究发现，该函数图象在第三象限内的最高点的坐标是（-2，-$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）当x＞0时，y随x的增大而增大．
